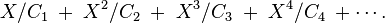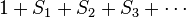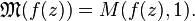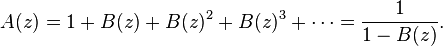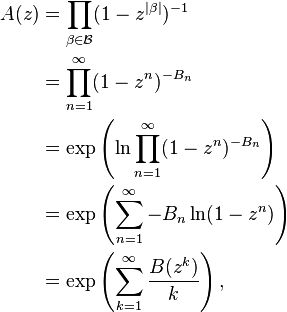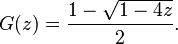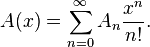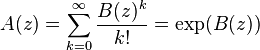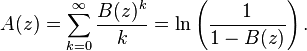Analytic combinatorics
In mathematics, analytic combinatorics is one of the many techniques of counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions and then complex analysis techniques to get asymptotics. This particular theory was mostly developed by Philippe Flajolet, and is detailed in his book with Robert Sedgewick, Analytic Combinatorics. Earlier contributors to the key ideas and techniques include Leonhard Euler, Arthur Cayley, Srinivasa Ramanujan, George Pólya, and Donald Knuth.
Classes of combinatorial structures
Consider the problem of distributing objects given by a generating function into a set of n slots, where a permutation group G of degree n acts on the slots to create an equivalence relation of filled slot configurations, and asking about the generating function of the configurations by weight of the configurations with respect to this equivalence relation, where the weight of a configuration is the sum of the weights of the objects in the slots. We will first explain how to solve this problem in the labelled and the unlabelled case and use the solution to motivate the creation of classes of combinatorial structures.
The Pólya enumeration theorem solves this problem in the unlabelled case. Let f(z) be the ordinary generating function (OGF) of the objects, then the OGF of the configurations is given by the substituted cycle index
In the labelled case we use an exponential generating function (EGF) g(z) of the objects and apply the Labelled enumeration theorem, which says that the EGF of the configurations is given by
We are able to enumerate filled slot configurations using either PET in the unlabelled case or the labelled enumeration theorem in the labelled case. We now ask about the generating function of configurations obtained when there is more than one set of slots, with a permutation group acting on each. Clearly the orbits do not intersect and we may add the respective generating functions. Suppose, for example, that we want to enumerate unlabelled sequences of length two or three of some objects contained in a set X. There are two sets of slots, the first one containing two slots, and the second one, three slots. The group acting on the first set is  , and on the second slot,
, and on the second slot, 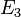 . We represent this by the following formal power series in X:
. We represent this by the following formal power series in X:
where the term  is used to denote the set of orbits under G and
is used to denote the set of orbits under G and  , which denotes in the obvious way the process of distributing the objects from X with repetition into the n slots. Similarly, consider the labelled problem of creating cycles of arbitrary length from a set of labelled objects X. This yields the following series of actions of cyclic groups:
, which denotes in the obvious way the process of distributing the objects from X with repetition into the n slots. Similarly, consider the labelled problem of creating cycles of arbitrary length from a set of labelled objects X. This yields the following series of actions of cyclic groups:
Clearly we can assign meaning to any such power series of quotients (orbits) with respect to permutation groups, where we restrict the groups of degree n to the conjugacy classes  of the symmetric group
of the symmetric group  , which form a unique factorization domain. (The orbits with respect to two groups from the same conjugacy class are isomorphic.) This motivates the following definition.
, which form a unique factorization domain. (The orbits with respect to two groups from the same conjugacy class are isomorphic.) This motivates the following definition.
A class ![\mathcal{C}\in \mathbb{N}[\mathfrak{A}]](../I/m/1e5d877824e8361154d8064e79b1120e.png) of combinatorial structures is a formal series
of combinatorial structures is a formal series
where  (the "A" is for "atoms") is the set of primes of the UFD
(the "A" is for "atoms") is the set of primes of the UFD  and
and 
In the following we will simplify our notation a bit and write e.g.
for the classes mentioned above.
The Flajolet–Sedgewick fundamental theorem
A theorem in the Flajolet–Sedgewick theory of symbolic combinatorics treats the enumeration problem of labelled and unlabelled combinatorial classes by means of the creation of symbolic operators that make it possible to translate equations involving combinatorial structures directly (and automatically) into equations in the generating functions of these structures.
Let ![\mathcal{C}\in\mathbb{N}[\mathfrak{A}]](../I/m/1e5d877824e8361154d8064e79b1120e.png) be a class of combinatorial structures. The OGF
be a class of combinatorial structures. The OGF  of
of 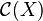 where X has OGF
where X has OGF  and the EGF
and the EGF  of
of 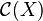 where X is labelled with EGF
where X is labelled with EGF 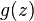 are given by
are given by
and
In the labelled case we have the additional requirement that X not contain elements of size zero. It will sometimes prove convenient to add one to  to indicate the presence of one copy of the empty set. It is possible to assign meaning to both
to indicate the presence of one copy of the empty set. It is possible to assign meaning to both ![\mathcal{C}\in\mathbb{Z}[\mathfrak{A}]](../I/m/9709a4cbcc664833e837341dea156d31.png) (the most common example is the case of unlabelled sets) and
(the most common example is the case of unlabelled sets) and ![\mathcal{C}\in\mathbb{Q}[\mathfrak{A}].](../I/m/b20c5741d3d1ffeb87dd323896f6b424.png) To prove the theorem simply apply PET (Pólya enumeration theorem) and the labelled enumeration theorem.
To prove the theorem simply apply PET (Pólya enumeration theorem) and the labelled enumeration theorem.
The power of this theorem lies in the fact that it makes it possible to construct operators on generating functions that represent combinatorial classes. A structural equation between combinatorial classes thus translates directly into an equation in the corresponding generating functions. Moreover in the labelled case it is evident from the formula that we may replace 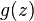 by the atom z and compute the resulting operator, which may then be applied to EGFs. We now proceed to construct the most important operators. The reader may wish to compare with the data on the cycle index page.
by the atom z and compute the resulting operator, which may then be applied to EGFs. We now proceed to construct the most important operators. The reader may wish to compare with the data on the cycle index page.
The sequence operator 
This operator corresponds to the class
and represents sequences, i.e. the slots are not being permuted and there is exactly one empty sequence. We have
and
The cycle operator 
This operator corresponds to the class
i.e., cycles containing at least one object. We have
or
and
This operator, together with the set operator 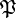 , and their restrictions to specific degrees are used to compute random permutation statistics. There are two useful restrictions of this operator, namely to even and odd cycles.
, and their restrictions to specific degrees are used to compute random permutation statistics. There are two useful restrictions of this operator, namely to even and odd cycles.
The labelled even cycle operator  is
is
which yields
This implies that the labelled odd cycle operator 
is given by
The multiset/set operator 
The series is
i.e., the symmetric group is applied to the slots. This creates multisets in the unlabelled case and sets in the labelled case (there are no multisets in the labelled case because the labels distinguish multiple instances of the same object from the set being put into different slots). We include the empty set in both the labelled and the unlabelled case.
The unlabelled case is done using the function
so that
Evaluating 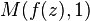 we obtain
we obtain
For the labelled case we have
In the labelled case we denote the operator by 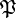 , and in the unlabelled case, by
, and in the unlabelled case, by  .
.
Procedure
Typically, one starts with the neutral class 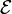 , containing a single object of size 0 (the neutral object, often denoted by
, containing a single object of size 0 (the neutral object, often denoted by  ), and one or more atomic classes
), and one or more atomic classes  , each containing a single object of size 1. Next, set-theoretic relations involving various simple operations, such as disjoint unions, products, sets, sequences, and multisets define more complex classes in terms of the already defined classes. These relations may be recursive. The elegance of symbolic combinatorics lies in that the set theoretic, or symbolic, relations translate directly into algebraic relations involving the generating functions.
, each containing a single object of size 1. Next, set-theoretic relations involving various simple operations, such as disjoint unions, products, sets, sequences, and multisets define more complex classes in terms of the already defined classes. These relations may be recursive. The elegance of symbolic combinatorics lies in that the set theoretic, or symbolic, relations translate directly into algebraic relations involving the generating functions.
In this article, we will follow the convention of using script uppercase letters to denote combinatorial classes and the corresponding plain letters for the generating functions (so the class  has generating function
has generating function  ).
).
There are two types of generating functions commonly used in symbolic combinatorics—ordinary generating functions, used for combinatorial classes of unlabelled objects, and exponential generating functions, used for classes of labelled objects.
It is trivial to show that the generating functions (either ordinary or exponential) for 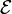 and
and  are
are  and
and 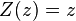 , respectively. The disjoint union is also simple — for disjoint sets
, respectively. The disjoint union is also simple — for disjoint sets  and
and  ,
,  implies
implies 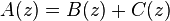 . The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).
. The relations corresponding to other operations depend on whether we are talking about labelled or unlabelled structures (and ordinary or exponential generating functions).
Combinatorial sum
The restriction of unions to disjoint unions is an important one; however, in the formal specification of symbolic combinatorics, it is too much trouble to keep track of which sets are disjoint. Instead, we make use of a construction that guarantees there is no intersection (be careful, however; this affects the semantics of the operation as well). In defining the combinatorial sum of two sets  and
and  , we mark members of each set with a distinct marker, for example
, we mark members of each set with a distinct marker, for example  for members of
for members of  and
and  for members of
for members of  . The combinatorial sum is then:
. The combinatorial sum is then:
This is the operation that formally corresponds to addition.
Unlabelled structures
With unlabelled structures, an ordinary generating function (OGF) is used. The OGF of a sequence  is defined as
is defined as
Product
The product of two combinatorial classes  and
and  is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for
is specified by defining the size of an ordered pair as the sum of the sizes of the elements in the pair. Thus we have for  and
and 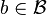 ,
,  . This should be a fairly intuitive definition. We now note that the number of elements in
. This should be a fairly intuitive definition. We now note that the number of elements in 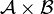 of size n is
of size n is
Using the definition of the OGF and some elementary algebra, we can show that
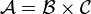 implies
implies 
Sequence
The sequence construction, denoted by  is defined as
is defined as
In other words, a sequence is the neutral element, or an element of  , or an ordered pair, ordered triple, etc. This leads to the relation
, or an ordered pair, ordered triple, etc. This leads to the relation
Set
The set (or powerset) construction, denoted by  is defined as
is defined as
which leads to the relation
where the expansion
was used to go from line 4 to line 5.
Multiset
The multiset construction, denoted  is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,
is a generalization of the set construction. In the set construction, each element can occur zero or one times. In a multiset, each element can appear an arbitrary number of times. Therefore,
This leads to the relation
where, similar to the above set construction, we expand  , swap the sums, and substitute for the OGF of
, swap the sums, and substitute for the OGF of  .
.
Other elementary constructions
Other important elementary constructions are:
- the cycle construction (
 ), like sequences except that cyclic rotations are not considered distinct
), like sequences except that cyclic rotations are not considered distinct - pointing (
 ), in which each member of
), in which each member of  is augmented by a neutral (zero size) pointer to one of its atoms
is augmented by a neutral (zero size) pointer to one of its atoms - substitution (
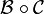 ), in which each atom in a member of
), in which each atom in a member of  is replaced by a member of
is replaced by a member of  .
.
The derivations for these constructions are too complicated to show here. Here are the results:
| Construction | Generating function |
|---|---|
 |
 (where (where  is the Euler totient function) is the Euler totient function) |
 |
 |
 |
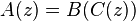 |
Examples
Many combinatorial classes can be built using these elementary constructions. For example, the class of plane trees (that is, trees embedded in the plane, so that the order of the subtrees matters) is specified by the recursive relation
In other words, a tree is a root node of size 1 and a sequence of subtrees. This gives
we solve for G(z) by multiplying  to get
to get

subtracting z and solving for G(z) using the quadratic formula gives
Another example (and a classic combinatorics problem) is integer partitions. First, define the class of positive integers  , where the size of each integer is its value:
, where the size of each integer is its value:
The OGF of  is then
is then
Now, define the set of partitions 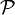 as
as
The OGF of 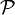 is
is
Unfortunately, there is no closed form for  ; however, the OGF can be used to derive a recurrence relation, or, using more advanced methods of analytic combinatorics, calculate the asymptotic behavior of the counting sequence.
; however, the OGF can be used to derive a recurrence relation, or, using more advanced methods of analytic combinatorics, calculate the asymptotic behavior of the counting sequence.
Labelled structures
An object is weakly labelled if each of its atoms has a nonnegative integer label, and each of these labels is distinct. An object is (strongly or well) labelled, if furthermore, these labels comprise the consecutive integers ![[1 \ldots n]](../I/m/56a2b8905c28bd647293a56a75cab7d6.png) . Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graphs.
. Note: some combinatorial classes are best specified as labelled structures or unlabelled structures, but some readily admit both specifications. A good example of labelled structures is the class of labelled graphs.
With labelled structures, an exponential generating function (EGF) is used. The EGF of a sequence  is defined as
is defined as
Product
For labelled structures, we must use a different definition for product than for unlabelled structures. In fact, if we simply used the cartesian product, the resulting structures would not even be well labelled. Instead, we use the so-called labelled product, denoted 
For a pair  and
and 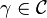 , we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in
, we wish to combine the two structures into a single structure. In order for the result to be well labelled, this requires some relabelling of the atoms in 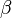 and
and  . We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.
. We will restrict our attention to relabellings that are consistent with the order of the original labels. Note that there are still multiple ways to do the relabelling; thus, each pair of members determines not a single member in the product, but a set of new members. The details of this construction are found on the page of the Labelled enumeration theorem.
To aid this development, let us define a function,  , that takes as its argument a (possibly weakly) labelled object
, that takes as its argument a (possibly weakly) labelled object  and relabels its atoms in an order-consistent way so that
and relabels its atoms in an order-consistent way so that 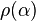 is well labelled. We then define the labelled product for two objects
is well labelled. We then define the labelled product for two objects  and
and 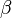 as
as
Finally, the labelled product of two classes  and
and  is
is
The EGF can be derived by noting that for objects of size  and
and  , there are
, there are  ways to do the relabelling. Therefore, the total number of objects of size
ways to do the relabelling. Therefore, the total number of objects of size  is
is
This binomial convolution relation for the terms is equivalent to multiplying the EGFs,
Sequence
The sequence construction  is defined similarly to the unlabelled case:
is defined similarly to the unlabelled case:
and again, as above,
Set
In labelled structures, a set of  elements corresponds to exactly
elements corresponds to exactly  sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for
sequences. This is different from the unlabelled case, where some of the permutations may coincide. Thus for  , we have
, we have
Cycle
Cycles are also easier than in the unlabelled case. A cycle of length  corresponds to
corresponds to  distinct sequences. Thus for
distinct sequences. Thus for  , we have
, we have
Boxed product
In labelled structures, the min-boxed product  is a variation of the original product which requires the element of
is a variation of the original product which requires the element of  in the product with the minimal label. Similarly, we can also define a max-boxed product, denoted by
in the product with the minimal label. Similarly, we can also define a max-boxed product, denoted by  , by the same manner. Then we have,
, by the same manner. Then we have,
or equivalently,
Example
An increasing Cayley tree is a labelled non-plane and rooted tree whose labels along any branch stemming from the root form an increasing sequence. Then, let  be the class of such trees. The recursive specification is now
be the class of such trees. The recursive specification is now 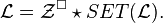
Other elementary constructions
The operators
represent cycles of even and odd length, and sets of even and odd cardinality.
Example
Stirling numbers of the second kind may be derived and analyzed using the structural decomposition
The decomposition
is used to study unsigned Stirling numbers of the first kind, and in the derivation of the statistics of random permutations. A detailed examination of the exponential generating functions associated to Stirling numbers within symbolic combinatorics may be found on the page on Stirling numbers and exponential generating functions in symbolic combinatorics.
See also
References
- François Bergeron, Gilbert Labelle, Pierre Leroux, Théorie des espèces et combinatoire des structures arborescentes, LaCIM, Montréal (1994). English version: Combinatorial Species and Tree-like Structures, Cambridge University Press (1998).
- Philippe Flajolet and Robert Sedgewick, Analytic Combinatorics, Cambridge University Press (2009). (available online: http://algo.inria.fr/flajolet/Publications/book.pdf)
- Micha Hofri, Analysis of Algorithms: Computational Methods and Mathematical Tools, Oxford University Press (1995).