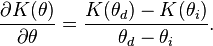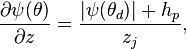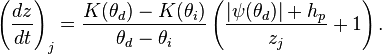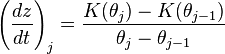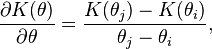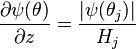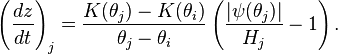Finite water-content vadose zone flow method
The finite water-content vadose zone flux method[1][2] represents a one-dimensional alternative to the numerical solution of Richards' equation [3] for simulating the movement of water in unsaturated soils. The finite water-content method is an ordinary differential equation alternative to the Richards partial differential equation. The Richards equation is difficult to approximate in general because it does not have a closed-form analytical solution except in a few cases.[4] The finite water-content method, is perhaps the first generic replacement for the numerical solution of the Richards' equation. The finite water-content solution has several advantages over the Richards equation solution. First, as an ordinary differential equation it is explicit, guaranteed to converge [5] and computationally inexpensive to solve. Second, using a finite volume solution methodology it is guaranteed to conserve mass. The finite water content method readily simulates sharp wetting fronts, something that the Richards solution struggles with.[6] The main limiting assumption required to use the finite water-content method is that the soil be homogeneous in layers.
 water content.
water content.The finite water-content vadose zone flux method is derived from the same starting point as the derivation of Richards' equation. However, the derivation employs a hodograph transformation[7] to produce an advection solution that does not include soil water diffusivity, wherein 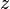 becomes the dependent variable and
becomes the dependent variable and  becomes an independent variable:[2]
becomes an independent variable:[2]
where:
 is the unsaturated hydraulic conductivity [L T−1],
is the unsaturated hydraulic conductivity [L T−1],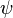 is the capillary pressure head [L] (negative for unsaturated soil),
is the capillary pressure head [L] (negative for unsaturated soil),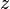 is the vertical coordinate [L] (positive downward),
is the vertical coordinate [L] (positive downward),  is the water content, (−) and
is the water content, (−) and is time [T].
is time [T].
This equation was converted into a set of three ordinary differential equations (ODEs) [2] using the Method of Lines[8] to convert the partial derivatives on the right-hand side of the equation into appropriate finite difference forms. These three ODEs represent the dynamics of infiltrating water, falling slugs, and capillary groundwater, respectively.
Derivation
The derivation of the 1-D finite water-content method equation for calculating vertical flux 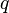 of water in the vadose zone starts with conservation of mass for an unsaturated porous medium without sources or sinks:
of water in the vadose zone starts with conservation of mass for an unsaturated porous medium without sources or sinks:
Next, the cyclic chain rule and chain rule are used to perform a hodograph transformation and convert the conservation of mass equation into a kinematic equation with z as the dependent variable[9]
We next insert the unsaturated Buckingham–Darcy flux:[10]
which yields:
The term on the far right-hand side of the above equation is negligible in the case of infiltration because we assume the soil has a delta-function diffusivity [11] so that 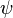 is constant along the infiltration wetting front.[2] Furthermore, evidence suggests that this term is small and negligible along the capillary groundwater wetting front when the groundwater table velocity is less than 0.92
is constant along the infiltration wetting front.[2] Furthermore, evidence suggests that this term is small and negligible along the capillary groundwater wetting front when the groundwater table velocity is less than 0.92 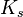 .[12] Therefore, the resulting finite water-content vadose zone flow equation is:
.[12] Therefore, the resulting finite water-content vadose zone flow equation is:
One way to solve this equation is to solve it for 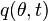 and
and 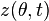 by integration:[13]
by integration:[13]
Instead, a finite water-content discretization is used and the integrals are replaced with summations:
where  is the total number of finite water content bins.
is the total number of finite water content bins.
Using this approach, the conservation equation for each bin is:
The method of lines is used to replace the partial differential forms on the right-hand side into appropriate finite-difference forms. This process results in a set of three ordinary differential equations that describe the dynamics of infiltration fronts, falling slugs, and groundwater capillary fronts using a finite water-content discretization.
Method essentials
The finite water-content vadose zone flux calculation method replaces the Richards' equation PDE with a set of three ordinary differential equations (ODEs). These three ODEs are developed in the following sections. Furthermore, because the finite water-content method does not explicitly include soil water diffusivity, it necessitates a separate capillary relaxation step. Capillary relaxation [14] represents a free-energy minimization process at the pore scale that produces no advection beyond the REV scale.
Infiltration fronts

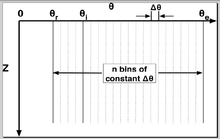
With reference to Figure 1, water infiltrating the land surface can flow through the pore space between 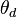 and
and  . In the context of the method of lines, the partial derivative terms are replaced with:
. In the context of the method of lines, the partial derivative terms are replaced with:
Given that any ponded depth of water on the land surface is 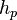 , the Green and Ampt (1911)[15] assumption is employed,
, the Green and Ampt (1911)[15] assumption is employed,
represents the capillary head gradient that is driving the flow. Therefore the finite water-content equation in the case of infiltration fronts is:
Falling slugs
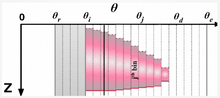
After rainfall stops and all surface water infiltrates, water in bins that contains infiltration fronts detaches from the land surface. Assuming that the capillarity at leading and trailing edges of this 'falling slug' of water is balanced, then the water falls through the media at the incremental conductivity associated with the 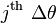 bin:
bin:
Capillary groundwater fronts

In this case, the flux of water to the 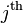 bin occurs between bin j and i. Therefore in the context of the method of lines:
bin occurs between bin j and i. Therefore in the context of the method of lines:
and,
which yields:
The performance of this equation was verified,[12] using a column experiment fashioned after that by Childs and Poulovassilis (1962).[16] Results of that validation showed that the finite water-content vadose zone flux calculation method performed comparably to the numerical solution of Richards' equation.
Capillary relaxation
Because the hydraulic conductivity rapidly increases as the water content moves towards saturation, with reference to Fig.1, right-most bins in both capillary groundwater fronts and infiltration fronts can "out-run" their neighbors to the left. In the finite water content discretization, these shocks[17] are dissipated by the process of capillary relaxation, which represents a pore-scale free-energy minimization process that produces no advection beyond the REV scale[14] Numerically, this process is a numerical sort that places the fronts in monotonically-decreasing magnitude from left-right.
Constitutive relations
The finite water content vadose zone flux method works with any monotonic water retention curve/unsaturated hydraulic conductivity relations such as Brooks and Corey[18] Clapp and Hornberger [19] and van Genuchten-Mualem.[20] The method might work with hysteretic water retention relations- these have not yet been tested.
Limitations
The finite water content method lacks the effect of soil water diffusion. Therefore, the shape of the wetting front plays no role in driving the flow. The method is therefore most suitable in coarser grain soils where advection is dominant over diffusion. The method is thus far limited to 1-D in practical applications. The infiltration equation [2] was extended to 2- and quasi-3 dimensions.[5] More work remains in extending the entire method into more than one dimension.
Demonstration video
https://www.youtube.com/watch?v=5aDPuhw9GJYof 8-month infiltration simulation from [2] 2600 mm of rain, evapotranspiration in 50 cm root zone, loam soil, and water table fixed at 1m depth. In the video, blue color denotes capillary groundwater, red color denotes infiltration fronts, and pink color denotes falling slugs.
References
- ↑ Talbot, C.A., and F. L. Ogden (2008), A method for computing infiltration and redistribution in a discretized moisture content domain, Water Resour. Res., 44(8), doi: 10.1029/2008WR006815.
- 1 2 3 4 5 6 Ogden, F. L., W. Lai, R. C. Steinke, J. Zhu, C. A. Talbot, and J. L. Wilson (2015), A new general 1-D vadose zone solution method, Water Resour.Res., 51, doi:10.1002/2015WR017126.
- ↑ Richards, L. A. (1931), Capillary conduction of liquids through porous mediums, J. Appl. Phys., 1(5), 318–333.
- ↑ Ross, P.J., and J.-Y. Parlange (1994). Comparing exact and numerical solutions of Richards equation for one-dimensional infiltration and drainage. Soil Sci. Vol 1557, No. 6, pp. 341-345.
- 1 2 Yu, H., C. C. Douglas, and F. L. Ogden, (2012), A new application of dynamic data driven system in the Talbot–Ogden model for groundwater infiltration, Procedia Computer Science, 9, 1073–1080.
- ↑ Tocci, M. D., C. T. Kelley, and C. T. Miller (1997), Accurate and economical solution of the pressure-head form of Richards' equation by the method of lines, Adv. Wat. Resour., 20(1), 1–14.
- ↑ Philip, J. R. 1957. The theory of infiltration: 1. The infiltration equation and its solution, Soil Sci, 83(5), 345–357.
- ↑ http://www.scholarpedia.org/article/Method_of_lines
- ↑ Philip, J. R., 1969., Theory of infiltration, Adv. Hydrosci., 5, 215–296.
- ↑ Jury, W. A., and R. Horton, 2004. Soil physics. John Wiley & Sons.
- ↑ Warrick A.W.. 2003. Soil Water Dynamics, Oxford Univ. Press, USA, pp. 159-162.
- 1 2 Ogden, F. L., W. Lai, R. C. Steinke, and J. Zhu (2015b), Validation of finite water-content vadose zone dynamics method using column experiments with a moving water table and applied surface flux, Water Resour. Res., 10.1002/2014WR016454.
- ↑ Wilson, J. L. (1974), Dispersive mixing in a partially saturated porous medium, PhD dissertation, 355pp., Dept. of Civil Engrg., Mass. Inst. Tech., Cambridge, MA.
- 1 2 Moebius, F., D. Canone, and D. Or (2012), Characteristics of acoustic emissions induced by fluid front displacement in porous media, Water Resour. Res., 48(11), W11507, doi:10.1029/2012WR012525.
- ↑ Green, W. H., and G. A. Ampt (1911), Studies on soil physics, 1, The flow of air and water through soils, J. Agric. Sci., 4(1), 1–24.
- ↑ Childs, E. C., and A. Poulovassilis (1962), The moisture profile above a moving water table, J. Soil Sci., 13(2), 271–285.
- ↑ Smith, R. E. (1983), Approximate soil water movement by kinematic characteristics, Soil Sci. Soc. Am. J., 47(1), 3–8.
- ↑ Brooks, R.H., and A.T. Corey, 1964. Hydraulic properties of porous media. Hydrol. Pap. 3, Colo. State Univ., Fort Collins, Colorado, USA.
- ↑ Clapp R.B., and G.M. Hornberger, 1978. Empirical equations for some soil hydraulic properties. Water Resour. Res. 14(4):601–604
- ↑ van Genuchten, M. Th. (1980). "A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils" (PDF). Soil Sci. Soc. Am. J., 44 (5): 892-898. doi:10.2136/sssaj1980.03615995004400050002x
![\left({\frac {dz}{dt}}\right)_{\theta }={\frac {\partial K(\theta )}{\partial \theta }}\left[1-\left({\frac {\partial \psi (\theta )}{\partial z}}\right)\right]\](../I/m/e6f9a22a5e84acac258756889b61938c.png)
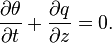
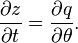
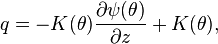
![{\frac {\partial q}{\partial \theta }}={\frac {\partial }{\partial \theta }}\left[K(\theta )\left(1-{\frac {\partial \psi (\theta )}{\partial z}}\right)\right]={\frac {\partial K(\theta )}{\partial \theta }}\left(1-{\frac {\partial \psi (\theta )}{\partial z}}\right)-K(\theta ){\frac {\partial ^{2}\psi (\theta )}{\partial z\,\partial \theta }}.](../I/m/0f5545d4810b6c836af4cddb0e842861.png)
![\left({\frac {dz}{dt}}\right)_{\theta }={\frac {\partial K(\theta )}{\partial \theta }}\left[1-\left({\frac {\partial \psi (\theta )}{\partial z}}\right)\right].](../I/m/21f0ccbf4876da60eb995f3a6cef9440.png)
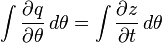
![\sum _{j=1}^{N}\left[{\frac {\partial q}{\partial \theta }}\right]_{j}\Delta \theta =\sum _{j=1}^{N}\left[{\frac {\partial z}{\partial t}}\right]_{j}\Delta \theta](../I/m/766d20825b4c8fdd2a505c57218a1be2.png)
![\left[{\frac {\partial q}{\partial \theta }}\right]_{j}=\left[{\frac {\partial z}{\partial t}}\right]_{j}.](../I/m/319e8712e81d24ca15b22f8df0b10fe9.png)