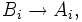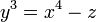Finite morphism

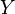In algebraic geometry, a branch of mathematics, a morphism $f: X \rightarrow Y$ of schemes is a finite morphism if $Y$ has an open cover by affine schemes

V_i = \mbox{Spec} \; B_i

such that for each $i$ ,

f^{-1}(V_i) = U_i

is an open affine subscheme 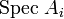$\mbox{Spec} \; A_i$ , and the restriction of f to $U_i$ , which induces a map of rings

B_i \rightarrow A_i,

makes $A_i$ a finitely generated module over $B_i$ .

Properties of finite morphisms

In the following, f : X → Y denotes a finite morphism.

The composition of two finite maps is finite.
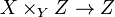Any base change of a finite morphism is finite, i.e. if $g: Z \rightarrow Y$ is another (arbitrary) morphism, then the canonical morphism $X \times_Y Z \rightarrow Z$ is finite. This corresponds to the following algebraic statement: if A is a finitely generated B-module, then the tensor product 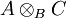$A \otimes_B C$ is a finitely generated C-module, where 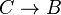$C \rightarrow B$ is any map. The generators are 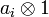$a_i \otimes 1$ , where $a_i$ are the generators of A as a B-module.
Closed immersions are finite, as they are locally given by 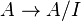$A \rightarrow A / I$ , where I is the ideal corresponding to the closed subscheme.
Finite morphisms are closed, hence (because of their stability under base change) proper. Indeed, replacing Y by the closure of f(X), one can assume that f is dominant. Further, one can assume that Y=Spec B is affine, hence so is X=Spec A. Then the morphism corresponds to an integral extension of rings B ⊂ A. Then the statement is a reformulation of the going up theorem of Cohen-Seidenberg.
Finite morphisms have finite fibres (i.e. they are quasi-finite). This follows from the fact that any finite k-algebra, for any field k is an Artinian ring. Slightly more generally, for a finite surjective morphism f, one has dim X=dim Y.
Conversely, proper, quasi-finite locally finite-presentation maps are finite. (EGA IV, 8.11.1.)
Finite morphisms are both projective and affine.

Morphisms of finite type

There is another finiteness condition on morphisms of schemes, morphisms of finite type, which is much weaker than being finite.

Morally, a morphism of finite type corresponds to a set of polynomial equations with finitely many variables. For example, the algebraic equation

y^3 = x^4 - z

corresponds to the map of (affine) schemes $\mbox{Spec} \; \mathbb Z [x, y, z] / \langle y^3-x^4+z \rangle \rightarrow \mbox{Spec} \; \mathbb Z$ or equivalently to the inclusion of rings $\mathbb Z \rightarrow \mathbb Z [x, y, z] / \langle y^3-x^4+z \rangle$ . This is an example of a morphism of finite type.

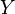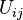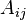The technical definition is as follows: let $\{V_i = \mbox{Spec} \; B_i\}$ be an open cover of $Y$ by affine schemes, and for each $i$ let $\{U_{ij} = \text{Spec} \; A_{ij}\}$ be an open cover of $f^{-1}(V_i)$ by affine schemes. The restriction of f to $U_{ij}$ induces a morphism of rings $B_i \rightarrow A_{ij}$ . The morphism f is called locally of finite type, if $A_{ij}$ is a finitely generated algebra over $B_i$ (via the above map of rings). 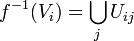If in addition the open cover $f^{-1}(V_i) = \bigcup_j U_{ij}$ can be chosen to be finite, then f is called of finite type.

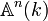For example, if $k$ is a field, the scheme $\mathbb{A}^n(k)$ has a natural morphism to 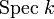$\text{Spec} \; k$ induced by the inclusion of rings $k \to k[X_1,\ldots,X_n].$ This is a morphism of finite type, but if $n \ge 1$ then it is not a finite morphism.

On the other hand, if we take the affine scheme ${\mbox{Spec}} \; k[X,Y]/ \langle Y^2-X^3-X \rangle$ , it has a natural morphism to $\mathbb{A}^1$ given by the ring homomorphism $k[X]\to k[X,Y]/ \langle Y^2-X^3-X \rangle.$ Then this morphism is a finite morphism.

References

Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157

This article is issued from Wikipedia - version of the Thursday, March 14, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Finite morphism

Properties of finite morphisms

Morphisms of finite type

See also

References