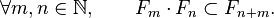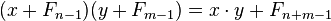Filtered algebra

In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory.

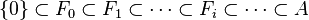A filtered algebra over the field k is an algebra (A,\cdot) over k which has an increasing sequence \{0\} \subset F_0 \subset F_1 \subset \cdots \subset F_i \subset \cdots \subset A of subspaces of A such that

A=\cup_{i\in \mathbb{N}} F_i

and that is compatible with the multiplication in the following sense

\forall m,n \in \mathbb{N},\qquad F_m\cdot F_n\subset F_{n+m}.

Associated graded algebra

In general there is the following construction that produces a graded algebra out of a filtered algebra.

If A is a filtered algebra then the associated graded algebra \mathcal{G}(A) is defined as follows:

  • As a vector space
    \mathcal{G}(A)=\bigoplus_{n\in \mathbb{N}}G_n\,,

    where,

    G_0=F_0, and
    \forall n>0, \quad G_n=F_n/F_{n-1}\,,
  • the multiplication is defined by
    (x+F_{n-1})(y+F_{m-1})=x\cdot y+F_{n+m-1}

    for all x\in F_n and y\in F_m. (More precisely, the multiplication map \mathcal{G}(A)\times \mathcal{G}(A) \to \mathcal{G}(A) is combined from the maps

    (F_n / F_{n-1}) \times (F_m / F_{m-1}) \to F_{n+m}/F_{n+m-1}, \ \ \ \ \ \left(x+F_{n-1},y+F_{m-1}\right) \mapsto x\cdot y+F_{n+m-1}
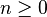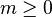    for all n\geq 0 and m\geq 0.)

The multiplication is well defined and endows \mathcal{G}(A) with the structure of a graded algebra, with gradation \{G_n\}_{n \in \mathbb{N}}. Furthermore if A is associative then so is \mathcal{G}(A). Also if A is unital, such that the unit lies in F_0, then \mathcal{G}(A) will be unital as well.

As algebras A and \mathcal{G}(A) are distinct (with the exception of the trivial case that A is graded) but as vector spaces they are isomorphic.

Examples

Any graded algebra graded by ℕ, for example 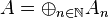A = \oplus_{n\in \mathbb{N}} A_n , has a filtration given by F_n = \oplus_{i=0}^n A_i .

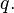An example of a filtered algebra is the Clifford algebra \mathrm{Cliff}(V,q) of a vector space V endowed with a quadratic form q. The associated graded algebra is 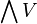\bigwedge V, the exterior algebra of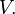 V.

The symmetric algebra on the dual of an affine space is a filtered algebra of polynomials; on a vector space, one instead obtains a graded algebra.

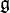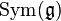The universal enveloping algebra of a Lie algebra \mathfrak{g} is also naturally filtered. The PBW theorem states that the associated graded algebra is simply \mathrm{Sym} (\mathfrak{g}).

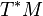Scalar differential operators on a manifold M form a filtered algebra where the filtration is given by the degree of differential operators. The associated graded algebra is the commutative algebra of smooth functions on the cotangent bundle T^*M which are polynomial along the fibers of the projection \pi\colon T^*M\rightarrow M.

The group algebra of a group with a length function is a filtered algebra.

See also

References

This article incorporates material from Filtered algebra on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the Wednesday, September 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.