Fifth-order Korteweg–de Vries equation

A fifth-order Korteweg–de Vries (KdV) equation is a nonlinear partial differential equation in 1+1 dimensions related to the Korteweg–de Vries equation.[1] Fifth order KdV equations may be used to model dispersive phenomena such as plasma waves when the third-order contributions are small. The term may refer to equations of the form

u_{t}+\alpha u_{xxx}+\beta u_{xxxxx} = \frac {\partial} {\partial x} f(u, u_{x}, u_{xx})

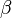where f is a smooth function and \alpha and \beta are real with \beta \neq 0. Unlike the KdV system, it is not integrable. It admits a great variety of soliton solutions.[2]

References

  1. ↑ Andrei D. Polyanin, Valentin F. Zaitsev, HANDBOOK of NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION p 1034, CRC PRESS
  2. ↑ "Stability and instability of solitary waves of the fifth-order KdV equation: a numerical framework" (PDF). Retrieved 8 May 2015.
This article is issued from Wikipedia - version of the Wednesday, July 01, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.