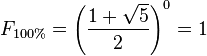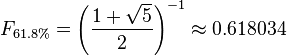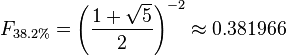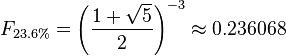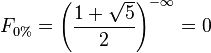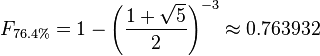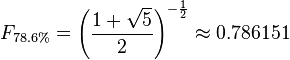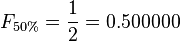Fibonacci retracement

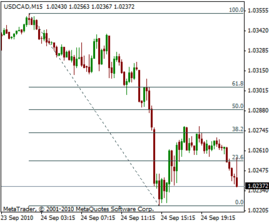
Fibonacci retracement levels shown on the USD/CAD currency pair
Fibonacci retracement levels shown on the USD/CAD currency pair. In this case, price retraced approximately 38.2% of a move down before continuing.

In finance, Fibonacci retracement is a method of technical analysis for determining support and resistance levels. They are named after their use of the Fibonacci sequence. Fibonacci retracement is based on the idea that markets will retrace a predictable portion of a move, after which they will continue to move in the original direction.

The appearance of retracement can be ascribed to ordinary price volatility as described by Burton Malkiel, a Princeton economist in his book A Random Walk Down Wall Street, who found no reliable predictions in technical analysis methods taken as a whole. Malkiel argues that asset prices typically exhibit signs of random walk and that one cannot consistently outperform market averages. Fibonacci retracement is created by taking two extreme points on a chart and dividing the vertical distance by the key Fibonacci ratios. 0.0% is considered to be the start of the retracement, while 100.0% is a complete reversal to the original part of the move. Once these levels are identified, horizontal lines are drawn and used to identify possible support and resistance levels.

Fibonacci ratios

Fibonacci ratios are mathematical relationships, expressed as ratios, derived from the Fibonacci sequence. The key Fibonacci ratios are 0%, 23.6%, 38.2%, 61.8%, and 100%.

F_{100\%} = \left(\frac{1 + \sqrt{5}}{2}\right)^{0} = 1 \,

The key Fibonacci ratio of 0.618 is derived by dividing any number in the sequence by the number that immediately follows it. For example: 8/13 is approximately 0.6154, and 55/89 is approximately 0.6180.

F_{61.8\%} = \left({\frac{1 + \sqrt{5}}{2}}\right)^{-1} \approx 0.618034 \,

The 0.382 ratio is found by dividing any number in the sequence by the number that is found two places to the right. For example: 34/89 is approximately 0.3820.

F_{38.2\%} = \left({\frac{1 + \sqrt{5}}{2}}\right)^{-2} \approx 0.381966 \,

The 0.236 ratio is found by dividing any number in the sequence by the number that is three places to the right. For example: 55/233 is approximately 0.2361.

F_{23.6\%} = \left({\frac{1 + \sqrt{5}}{2}}\right)^{-3} \approx 0.236068 \,

The 0 ratio is :

F_{0\%} = \left({\frac{1 + \sqrt{5}}{2}}\right)^{-\infty} = 0 \,

Other ratios

The 0.764 ratio is the result of subtracting 0.236 from the number 1.

F_{76.4\%} = 1- \left({\frac{1 + \sqrt{5}}{2}}\right)^{-3} \approx 0.763932 \,

The 0.786 ratio is :

F_{78.6\%} = \left({\frac{1 + \sqrt{5}}{2}}\right)^{-\frac{1}{2}} \approx 0.786151 \,

The 0.500 ratio is derived from dividing the number 1 (second number in the sequence) by the number 2 (third number in the sequence).

F_{50\%} = \frac{1}{2} = 0.500000 \,

Academic studies

Bhattacharya, Sukanto and Kumar, Kuldeep (2006) A computational exploration of the efficacy of Fibonacci sequences in technical analysis and trading. Annals of Economics and Finance, Volume 7, Issue 1, May 2006, pp. 219-230. http://epublications.bond.edu.au/business_pubs/32/

Chatterjee, Amitava, O. Felix Ayadi, and Balasundram Maniam. "The Applications Of The Fibonacci Sequence And Elliott Wave Theory In Predicting The Security Price Movements: A Survey." Journal of Commercial Banking and Finance 1 (2002): 65-76.

Tai-Liang Chena, Ching-Hsue Chenga, Hia Jong Teoha. Fuzzy time-series based on Fibonacci sequence for stock price forecasting. Physica A: Statistical Mechanics and its Applications, Volume 380, 1 July 2007, Pages 377–390.

References

    External links

    This article is issued from Wikipedia - version of the Sunday, January 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.