Fibered knot

Figure-eight knot is fibered.

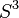In knot theory, a branch of mathematics, a knot or link K in the 3-dimensional sphere S^3 is called fibered or fibred (sometimes Neuwirth knot in older texts, after Lee Neuwirth) if there is a 1-parameter family F_t of Seifert surfaces for K, where the parameter t runs through the points of the unit circle S^1, such that if s is not equal to t then the intersection of 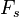F_s and F_t is exactly K.

For example:

Fibered knots and links arise naturally, but not exclusively, in complex algebraic geometry. For instance, each singular point of a complex plane curve can be described topologically as the cone on a fibered knot or link called the link of the singularity. The trefoil knot is the link of the cusp singularity 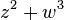z^2+w^3; the Hopf link (oriented correctly) is the link of the node singularity 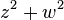z^2+w^2. In these cases, the family of Seifert surfaces is an aspect of the Milnor fibration of the singularity.

A knot is fibered if and only if it is the binding of some open book decomposition of 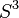S^3.

Knots that are not fibered

Stevedore's knot is not fibered

The Alexander polynomial of a fibered knot is monic, i.e. the coefficients of the highest and lowest powers of t are plus or minus 1. Examples of knots with nonmonic Alexander polynomials abound, for example the twist knots have Alexander polynomials qt − (2q + 1) + qt−1, where q is the number of half-twists.[1] In particular the Stevedore's knot is not fibered.

See also

References

  1. ↑ "[dg-ga/9612014] Knots, Links, and 4-Manifolds". Arxiv.org. Retrieved 2014-04-19.

External links


This article is issued from Wikipedia - version of the Friday, March 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.