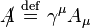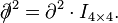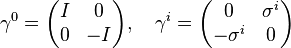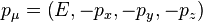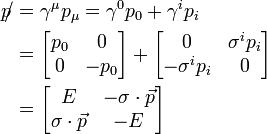Feynman slash notation
In the study of Dirac fields in quantum field theory, Richard Feynman invented the convenient Feynman slash notation (less commonly known as the Dirac slash notation[1]). If A is a covariant vector (i.e., a 1-form),
using the Einstein summation notation where γ are the gamma matrices.
Identities
Using the anticommutators of the gamma matrices, one can show that for any  and
and 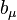 ,
,

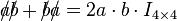 .
.
where 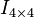 is the identity matrix in four dimensions.
In particular,
is the identity matrix in four dimensions.
In particular,
Further identities can be read off directly from the gamma matrix identities by replacing the metric tensor with inner products. For example,
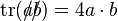
![\operatorname{tr}(a\!\!\!/b\!\!\!/c\!\!\!/d\!\!\!/) = 4 \left[(a\cdot b)(c \cdot d) - (a \cdot c)(b \cdot d) + (a \cdot d)(b \cdot c) \right]](../I/m/e693cc094863470e8384be72832717fb.png)
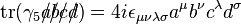
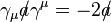 .
.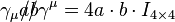
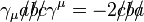
- where
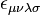 is the Levi-Civita symbol.
is the Levi-Civita symbol.
With four-momentum
Often, when using the Dirac equation and solving for cross sections, one finds the slash notation used on four-momentum:
using the Dirac basis for the 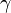 's,
's,
as well as the definition of four momentum
We see explicitly that
Similar results hold in other bases, such as the Weyl basis.
See also
References
- ↑ Weinberg, Steven (1995), The Quantum Theory of Fields 1, Cambridge University Press, p. 358 (380 in polish edition), ISBN 0-521-55001-7
- Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.