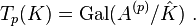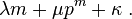Ferrero–Washington theorem

In algebraic number theory, the Ferrero–Washington theorem, proved first by Ferrero & Washington (1979) and later by Sinnott (1984), states that Iwasawa's μ-invariant vanishes for cyclotomic Z_p-extensions of abelian algebraic number fields.

History

Iwasawa (1959) introduced the μ-invariant of a Z_p-extension and observed that it was zero in all cases he calculated. Iwasawa & Sims (1966) used a computer to check that it vanishes for the cyclotomic Z_p-extension of the rationals for all primes less than 4000. Iwasawa (1971) later conjectured that the μ-invariant vanishes for any Z_p-extension, but shortly after Iwasawa (1973) discovered examples of non-cyclotomic extensions of number fields with non-vanishing μ-invariant showing that his original conjecture was wrong. He suggested, however, that the conjecture might still hold for cyclotomic Z_p-extensions.

Iwasawa (1958) showed that the vanishing of the μ-invariant for cyclotomic Z_p-extensions of the rationals is equivalent to certain congruences between Bernoulli numbers, and Ferrero & Washington (1979) showed that the μ-invariant vanishes in these cases by proving that these congruences hold.

Statement

For a number field K we let K_m denote the extension by p^m-power roots of unity, 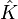$\hat K$ the union of the K_m and A^(p) the maximal unramified abelian p-extension of 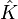$\hat K$ . Let the Tate module

T_p(K) = \mathrm{Gal}(A^{(p)}/\hat K) \ .

Then T_p(K) is a pro-p-group and so a Z_p-module. Using class field theory one can describe T_p(K) as isomorphic to the inverse limit of the class groups C_m of the K_m under norm.^[1]

Iwasawa exhibited T_p(K) as a module over the completion Z_p''T'' and this implies a formula for the exponent of p in the order of the class groups C_m of the form

\lambda m + \mu p^m + \kappa \ .

The Ferrero–Washington theorem states that μ is zero.^[2]

References

↑ Manin & Panchishkin 2007, p. 245
↑ Manin & Panchishkin 2007, p. 246

Ferrero, Bruce; Washington, Lawrence C. (1979), "The Iwasawa invariant μ_p vanishes for abelian number fields", Annals of Mathematics. Second Series 109 (2): 377–395, doi:10.2307/1971116, ISSN 0003-486X, MR 528968, Zbl 0443.12001
Iwasawa, Kenkichi (1958), "On some invariants of cyclotomic fields", American Journal of Mathematics 81: 280, doi:10.2307/2372857, ISSN 0002-9327, MR 0124317[http://www.jstor.org/stable/2372857 correction]
Iwasawa, Kenkichi (1959), "On Γ-extensions of algebraic number fields", Bulletin of the American Mathematical Society 65 (4): 183–226, doi:10.1090/S0002-9904-1959-10317-7, ISSN 0002-9904, MR 0124316
Iwasawa, Kenkichi (1971), "On some infinite Abelian extensions of algebraic number fields", Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, Gauthier-Villars, pp. 391–394, MR 0422205
Iwasawa, Kenkichi (1973), "On the μ-invariants of Z1-extensions", Number theory, algebraic geometry and commutative algebra, in honor of Yasuo Akizuki, Tokyo: Kinokuniya, pp. 1–11, MR 0357371
Iwasawa, Kenkichi; Sims, Charles C. (1966), "Computation of invariants in the theory of cyclotomic fields", Journal of the Mathematical Society of Japan 18: 86–96, doi:10.4099/jmath.18.86, ISSN 0025-5645, MR 0202700
Manin, Yu. I.; Panchishkin, A. A. (2007), Introduction to Modern Number Theory, Encyclopaedia of Mathematical Sciences 49 (Second ed.), ISBN 978-3-540-20364-3, ISSN 0938-0396, Zbl 1079.11002
Sinnott, W. (1984), "On the μ-invariant of the Γ-transform of a rational function", Inventiones Mathematicae 75 (2): 273–282, doi:10.1007/BF01388565, ISSN 0020-9910, MR 732547, Zbl 0531.12004

This article is issued from Wikipedia - version of the Thursday, September 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.