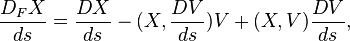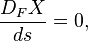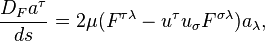Fermi–Walker transport
Fermi–Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame.
Fermi–Walker differentiation
In the theory of Lorentzian manifolds, Fermi–Walker differentiation is a generalization of covariant differentiation. In general relativity, Fermi–Walker derivatives of the spacelike unit vector fields in a frame field, taken with respect to the timelike unit vector field in the frame field, are used to define non-inertial but nonspinning frames, by stipulating that the Fermi–Walker derivatives should vanish. In the special case of inertial frames, the Fermi–Walker derivatives reduce to covariant derivatives.
With a  sign convention, this is defined for a vector field X along a curve
sign convention, this is defined for a vector field X along a curve 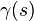 :
:
where V is four-velocity, D is the covariant derivative in the Riemannian space, and (,) is scalar product. If
the vector field X is Fermi–Walker transported along the curve (see Hawking and Ellis, p. 80). Vectors perpendicular to the space of four-velocities in Minkowski spacetime, e.g., polarization vectors, under Fermi–Walker transport experience Thomas precession.
Using the Fermi derivative, the Bargmann–Michel–Telegdi equation[1] for spin precession of electron in an external electromagnetic field can be written as follows:
where 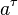 and
and 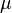 are polarization four-vector and magnetic moment,
are polarization four-vector and magnetic moment, 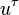 is four-velocity of electron,
is four-velocity of electron, 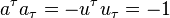 ,
, 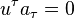 , and
, and 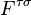 is electromagnetic field-strength tensor. The right side describes Larmor precession.
is electromagnetic field-strength tensor. The right side describes Larmor precession.
Co-moving coordinate systems
A coordinate system co-moving with the particle can be defined. If we take the unit vector 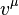 as defining an axis in the co-moving coordinate system, then any system transforming with proper time is said to be undergoing Fermi Walker transport.[2]
as defining an axis in the co-moving coordinate system, then any system transforming with proper time is said to be undergoing Fermi Walker transport.[2]
See also
- Basic introduction to the mathematics of curved spacetime
- Enrico Fermi
- Transition from Newtonian mechanics to general relativity
References
- ↑ V. Bargmann, L. Michel, and V. L. Telegdi, Precession of the Polarization of Particles Moving in a Homogeneous Electromagnetic Field, Phys. Rev. Lett. 2, 435 (1959).
- ↑ Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. p. 170. ISBN 0-7167-0344-0.
Textbooks
- Landau, L. D. and Lifshitz, E. M. (1975). Classical Theory of Fields (Fourth Revised English Edition). Oxford: Pergamon. ISBN 0-08-018176-7.
| ||||||||||||||||||||||||||