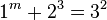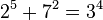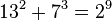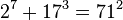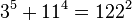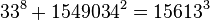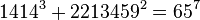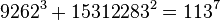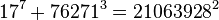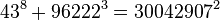Fermat–Catalan conjecture
In number theory, the Fermat–Catalan conjecture combines ideas of Fermat's last theorem and the Catalan conjecture, hence the name. The conjecture states that the equation
-
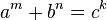
(1)
-
has only finitely many solutions (a,b,c,m,n,k) with distinct triplets of values (am, bn, ck); here a, b, c are positive coprime integers and m, n, k are positive integers satisfying
-
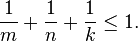
(2)
-
This inequality restriction on the exponents has the effect of precluding consideration of the known infinitude of solutions of (1) in which two of the exponents are 2 (such as Pythagorean triples).
As of 2015, the following ten solutions to (1) are known:[1]
The first of these (1m+23=32) is the only solution where one of a, b or c is 1, according to the Catalan conjecture, proven in 2002 by Preda Mihăilescu. While this case leads to infinitely many solutions of (1) (since we can pick any m for m>5), these solutions only give a single triplet of values (am, bn, ck).
It is known by Faltings' theorem that for any fixed choice of positive integers m, n and k satisfying (2), only finitely many coprime triples (a, b, c) solving (1) exist, but of course the full Fermat–Catalan conjecture is a much stronger statement since it allows for an infinitude of sets of exponents m, n and k.
The abc conjecture implies the Fermat–Catalan conjecture.[1]
Beal's conjecture is true if and only if all Fermat-Catalan solutions use 2 as an exponent for some variable.
See also
- Sums of powers, a list of related conjectures and theorems
References
- 1 2 Pomerance, Carl (2008), "Computational Number Theory", in Gowers, Timothy; Barrow-Green, June; Leader, Imre, The Princeton Companion to Mathematics, Princeton University Press, pp. 361–362, ISBN 978-0-691-11880-2.