Feit–Thompson conjecture
In mathematics, the Feit–Thompson conjecture is a conjecture in number theory, suggested by Walter Feit and John G. Thompson (1962). The conjecture states that there are no distinct prime numbers p and q such that
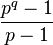divides 
.
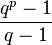If the conjecture were true, it would greatly simplify the final chapter of the proof (Feit & Thompson 1963) of the Feit–Thompson theorem that every finite group of odd order is solvable. A stronger conjecture that the two numbers are always coprime was disproved by Stephens (1971) with the counterexample p = 17 and q = 3313 with common factor 2pq + 1 = 112643.
Informal probability arguments suggest that the "expected" number of counterexamples to the Feit–Thompson conjecture is very close to 0, suggesting that the Feit–Thompson conjecture is likely to be true.
See also
References
- Feit, Walter; Thompson, John G. (1962), "A solvability criterion for finite groups and some consequences", Proc. Nat. Acad. Sci. U.S.A. 48 (6): 968–970, doi:10.1073/pnas.48.6.968, JSTOR 71265 MR 0143802
- Feit, Walter; Thompson, John G. (1963), "Solvability of groups of odd order", Pacific J. Math. 13: 775–1029, doi:10.2140/pjm.1963.13.775, ISSN 0030-8730, MR 0166261
- Stephens, Nelson M. (1971), "On the Feit–Thompson conjecture", Math. Comp. 25: 625, doi:10.2307/2005226, JSTOR 2005226, MR 0297686
External links
- Weisstein, Eric W., "Feit–Thompson Conjecture", MathWorld. (This article confuses the Feit–Thompson conjecture with the stronger disproved conjecture mentioned above.)