FastICA

FastICA is an efficient and popular algorithm for independent component analysis invented by Aapo Hyvärinen at Helsinki University of Technology.^[1]^[2] Like most ICA algorithms, FastICA seeks an orthogonal rotation of prewhitened data, through a fixed-point iteration scheme, that maximizes a measure of non-Gaussianity of the rotated components. Non-gaussianity serves as a proxy for statistical independence, which is a very strong condition and requires infinite data to verify. FastICA can also be alternatively derived as an approximative Newton iteration.

Algorithm

Prewhitening the data

Let the $\mathbf{x} := (x_{ij}) \in \mathbb{R}^{N \times M}$ denote the input vector data matrix. The columns of ${\mathbf x}$ correspond to $M$ observed mixed vectors of dimension $N$ . The input data matrix 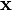$\mathbf{x}$ must be prewhitened, or centered and whitened, before applying the FastICA algorithm to it.

Centering the data entails demeaning each component of the input data 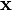$\mathbf{x}$ , that is,

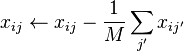
x_{ij} \leftarrow x_{ij} - \frac{1}{M} \sum_{j^{\prime}} x_{ij^{\prime}}

for each

i =1,\ldots,N

and

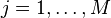j = 1, \ldots, M

. After centering, each row of

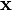\mathbf{x}

has an expected value of

0

Whitening the data requires a linear transformation 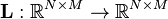$\mathbf{L}: \mathbb{R}^{N \times M} \to \mathbb{R}^{N \times M}$ of the centered data so that the components of 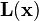$\mathbf{L}(\mathbf{x})$ are uncorrelated and have variance one. More precisely, if 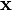$\mathbf{x}$ is a centered data matrix, the covariance of 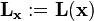$\mathbf{L}_{\mathbf{x}} := \mathbf{L}(\mathbf{x})$ is the 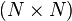$(N \times N)$ -dimensional identity matrix, that is,

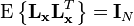
\mathrm{E}\left \{ \mathbf{L}_{\mathbf{x}} \mathbf{L}_{\mathbf{x}}^{T} \right \} = \mathbf{I}_N

A common method for whitening is by performing a eigenvalue decomposition on the covariance matrix of the centered data

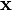\mathbf{x}

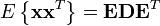E\left \{ \mathbf{x} \mathbf{x}^{T} \right \} = \mathbf{E}\mathbf{D}\mathbf{E}^T

, where

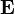\mathbf{E}

is the matrix of eigenvectors and

\mathbf{D}

is the diagonal matrix of eigenvalues. The whitened data matrix is defined thus by

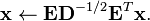
\mathbf{x} \leftarrow \mathbf{E}\mathbf{D}^{-1/2}\mathbf{E}^T\mathbf{x}.

Single component extraction

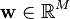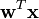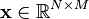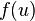The iterative algorithm finds the direction for the weight vector $\mathbf{w} \in \mathbb{R}^M$ that maximizes a measure of non-Gaussianity of the projection $\mathbf{w}^T \mathbf{x}$ , with $\mathbf{x} \in \mathbb{R}^{N \times M}$ denoting a prewhitened data matrix as described above. To measure non-Gaussianity, FastICA relies on a nonquadratic nonlinearity function $f(u)$ , its first derivative 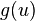$g(u)$ , and its second derivative 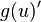$g(u)^{\prime}$ . Hyvärinen states that the functions

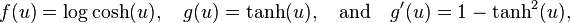
f(u) = \log \cosh (u), \quad g(u) = \tanh (u), \quad \text{and} \quad {g}'(u) = 1-\tanh^2(u),

are useful for general purposes, while

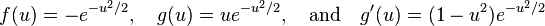
f(u) = -e^{-u^2/2}, \quad g(u) = u e^{-u^2/2}, \quad \text{and} \quad {g}'(u) = (1-u^2) e^{-u^2/2}

may be highly robust.^[1] The steps for extracting the weight vector $\mathbf{w}$ for single component in FastICA are the following.

Randomize the initial weight vector $\mathbf{w}$
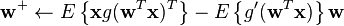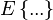Let $\mathbf{w}^+ \leftarrow E\left\{\mathbf{x} g(\mathbf{w}^T \mathbf{x})^T\right\} - E\left\{g'(\mathbf{w}^T \mathbf{x})\right\}\mathbf{w}$ , where $E\left\{...\right\}$ means averaging over all column-vectors of matrix $\mathbf{X}$
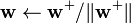
Let $\mathbf{w} \leftarrow \mathbf{w}^+ / \|\mathbf{w}^+\|$
If not converged, go back to 2

Multiple component extraction

The single unit iterative algorithm estimates only one weight vector which extracts a single component. Estimating additional components that are mutually "independent" requires repeating the algorithm to obtain linearly independent projection vectors - note that the notion of independence here refers to maximizing non-Gaussianity in the estimated components. Hyvärinen provides several ways of extracting multiple components with the simplest being the following. Here, $\mathbf{1}$ is a column vector of 1's of dimension M.

Algorithm FastICA

Input:

C

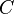Number of desired components

Input:

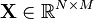\mathbf{X} \in \mathbb{R}^{N \times M}

Matrix, where each column represents an N-dimensional sample, where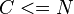

C <= N

Output:

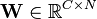\mathbf{W} \in \mathbb{R}^{C \times N}

Un-mixing matrix where each row projects X onto into independent component.

Output:

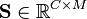\mathbf{S} \in \mathbb{R}^{C \times M}

Independent components matrix, with M columns representing a sample with C dimensions.

for p in 1 to C:
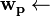     $\mathbf{w_p} \leftarrow$  Random vector of length N
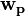    while  $\mathbf{w_p}$  changes
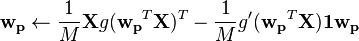
         $\mathbf{w_p} \leftarrow \frac{1}{M}\mathbf{X} g(\mathbf{w_p}^T \mathbf{X})^T - \frac{1}{M}g'(\mathbf{w_p}^T\mathbf{X})\mathbf{1} \mathbf{w_p}$ 
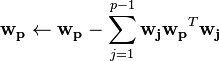
         $\mathbf{w_p} \leftarrow \mathbf{w_p} - \sum_{j = 1}^{p-1} \mathbf{w_j}\mathbf{w_p}^T\mathbf{w_j}$ 
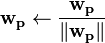         $\mathbf{w_p} \leftarrow \frac{\mathbf{w_p}}{\|\mathbf{w_p}\|}$ 
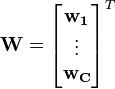Output:  $\mathbf{W} = \begin{bmatrix} \mathbf{w_1} \\ \vdots \\ \mathbf{w_C} \end{bmatrix}^T$ 
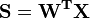
Output:  $\mathbf{S} = \mathbf{W^T}\mathbf{X}$

References

1 2 Hyvärinen, A.; Oja, E. (2000). "Independent component analysis: Algorithms and applications" (PDF). Neural Networks 13 (4–5): 411–430. doi:10.1016/S0893-6080(00)00026-5. PMID 10946390.
↑ Hyvarinen, A. (1999). "Fast and robust fixed-point algorithms for independent component analysis" (PDF). IEEE Transactions on Neural Networks 10 (3): 626–634. doi:10.1109/72.761722. PMID 18252563.

External links

This article is issued from Wikipedia - version of the Sunday, January 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.