Factorization system
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.
Definition
A factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that:
- E and M both contain all isomorphisms of C and are closed under composition.
- Every morphism f of C can be factored as
 for some morphisms
for some morphisms  and
and  .
. - The factorization is functorial: if
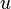 and
and 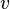 are two morphisms such that
are two morphisms such that 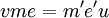 for some morphisms
for some morphisms  and
and  , then there exists a unique morphism
, then there exists a unique morphism  making the following diagram commute:
making the following diagram commute:

Remark:  is a morphism from
is a morphism from 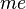 to
to  in the arrow category.
in the arrow category.
Orthogonality
Two morphisms  and
and  are said to be orthogonal, denoted
are said to be orthogonal, denoted 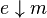 , if for every pair of morphisms
, if for every pair of morphisms 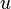 and
and 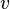 such that
such that  there is a unique morphism
there is a unique morphism  such that the diagram
such that the diagram

commutes. This notion can be extended to define the orthogonals of sets of morphisms by
 and
and 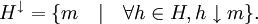
Since in a factorization system 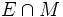 contains all the isomorphisms, the condition (3) of the definition is equivalent to
contains all the isomorphisms, the condition (3) of the definition is equivalent to
- (3')
 and
and 
Proof: In the previous diagram (3), take  (identity on the appropriate object) and
(identity on the appropriate object) and  .
.
Equivalent definition
The pair 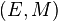 of classes of morphisms of C is a factorization system if and only if it satisfies the following conditions:
of classes of morphisms of C is a factorization system if and only if it satisfies the following conditions:
- Every morphism f of C can be factored as
 with
with  and
and 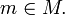
 and
and 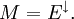
Weak factorization systems
Suppose e and m are two morphisms in a category C. Then e has the left lifting property with respect to m (resp. m has the right lifting property with respect to e) when for every pair of morphisms u and v such that ve=mu there is a morphism w such that the following diagram commutes. The difference with orthogonality is that w is not necessarily unique.

A weak factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that :
- The class E is exactly the class of morphisms having the left lifting property wrt the morphisms of M.
- The class M is exactly the class of morphisms having the right lifting property wrt the morphisms of E.
- Every morphism f of C can be factored as
 for some morphisms
for some morphisms  and
and  .
.
References
- Peter Freyd, Max Kelly (1972). "Categories of Continuous Functors I". Journal of Pure and Applied Algebra 2.
- Notes, Factorization Systems, Emily Riehl, 2008