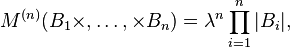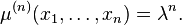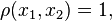Factorial moment measure
| Probability |
|---|
 |
In probability and statistics, a factorial moment measure is a mathematical quantity, function or, more precisely, measure that is defined in relation to mathematical objects known as point processes, which are types of stochastic processes often used as mathematical models of physical phenomena representable as randomly positioned points in time, space or both. Moment measures generalize the idea of factorial moments, which are useful for studying non-negative integer-valued random variables.[1]
The first factorial moment measure of a point process coincides with its first moment measure or intensity measure,[2] which gives the expected or average number of points of the point process located in some region of space. In general, if the number of points in some region is considered as a random variable, then the moment factorial measure of this region is the factorial moment of this random variable.[3] Factorial moment measures completely characterize a wide class of point processes, which means they can be used to uniquely identify a point process.
If a factorial moment measure is absolutely continuous, then with respect to the Lebesgue measure it is said to have a density (which is a generalized form of a derivative), and this density is known by a number of names including factorial moment density, product density, coincidence density,[1] joint intensity[4] , correlation function or multivariate frequency spectrum[5] The first and second factorial moment densities of a point process are used in the definition of the pair correlation function, which gives a way to statistically quantify the strength of interaction or correlation between points of a point process.[6]
Factorial moment measures serve as useful tools in the study of point processes[1][6][7] as well as the related fields of stochastic geometry[3] and spatial statistics,[6][8] which are applied in various scientific and engineering disciplines such as biology, geology, physics, and telecommunications.[1][3][9]
Point process notation
Point processes are mathematical objects that are defined on some underlying mathematical space. Since these processes are often used to represent collections of points randomly scattered in space, time or both, the underlying space is usually d-dimensional Euclidean space denoted here by Rd, but they can be defined on more abstract mathematical spaces.[7]
Point processes have a number of interpretations, which is reflected by the various types of point process notation.[3][9] For example, if a point  belongs to or is a member of a point process, denoted by N, then this can be written as:[3]
belongs to or is a member of a point process, denoted by N, then this can be written as:[3]
and represents the point process being interpreted as a random set. Alternatively, the number of points of N located in some Borel set B is often written as:[2][3][8]
which reflects a random measure interpretation for point processes. These two notations are often used in parallel or interchangeably.[3][8][2]
Definitions
n th factorial power of a point process
For some positive integer 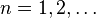 , the
, the  -th factorial power of a point process
-th factorial power of a point process 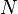 on
on 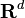 is defined as:[2]
is defined as:[2]
where 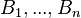 is a collection of not necessarily disjoint Borel sets in
is a collection of not necessarily disjoint Borel sets in 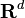 , which form a
, which form a  -fold Cartesian product of sets denoted by:
-fold Cartesian product of sets denoted by:
The symbol 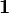 denotes an indicator function such that
denotes an indicator function such that 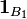 is a Dirac measure for the set
is a Dirac measure for the set 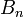 . The summation in the above expression is performed over all
. The summation in the above expression is performed over all  -tuples of distinct points, including permutations, which can be contrasted with the definition of the n-th power of a point process. The symbol
-tuples of distinct points, including permutations, which can be contrasted with the definition of the n-th power of a point process. The symbol 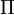 denotes multiplication while the existence of various point process notation means that the n-th factorial power of a point process is sometimes defined using other notation.[2]
denotes multiplication while the existence of various point process notation means that the n-th factorial power of a point process is sometimes defined using other notation.[2]
n th factorial moment measure
The n th factorial moment measure or n th order factorial moment measure is defined as:
where the E denotes the expectation (operator) of the point process N. In other words, the n-th factorial moment measure is the expectation of the n th factorial power of some point process.
The n th factorial moment measure of a point process N is equivalently defined[3] by:
where f is any non-negative measurable function on Rnd, and the above summation is performed over all n tuples of distinct points, including permutations. Consequently, the factorial moment measure is defined such that there are no points repeating in the product set, as opposed to the moment measure.[7]
First factorial moment measure
The first factorial moment measure 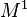 coincides with the first moment measure:[2]
coincides with the first moment measure:[2]
where 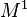 is known, among other terms, as the intensity measure[3] or mean measure,[10] and is interpreted as the expected number of points of
is known, among other terms, as the intensity measure[3] or mean measure,[10] and is interpreted as the expected number of points of 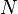 found or located in the set
found or located in the set 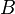
Second factorial moment measure
The second factorial moment measure for two Borel sets 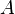 and
and 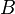 is:
is:
Name explanation
For some Borel set 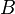 , the namesake of this measure is revealed when the
, the namesake of this measure is revealed when the 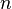 th factorial moment measure reduces to:
th factorial moment measure reduces to:
which is the 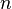 -th factorial moment of the random variable
-th factorial moment of the random variable 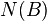 .[3]
.[3]
Factorial moment density
If a factorial moment measure is absolutely continuous, then it has a density (or more precisely, a Radon–Nikodym derivative or density) with respect to the Lebesgue measure and this density is known as the factorial moment density or product density, joint intensity, correlation function, or multivariate frequency spectrum. Denoting the  -th factorial moment density by
-th factorial moment density by 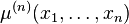 , it is defined in respect to the equation:[3]
, it is defined in respect to the equation:[3]
Furthermore, this means the following expression
where  is any non-negative bounded measurable function defined on
is any non-negative bounded measurable function defined on 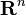 .
.
Pair correlation function
In spatial statistics and stochastic geometry, to measure the statistical correlation relationship between points of a point process, the pair correlation function of a point process  is defined as:[3][6]
is defined as:[3][6]
where the points 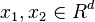 . In general,
. In general, 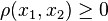 whereas
whereas 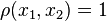 corresponds to no correlation (between points) in the typical statistical sense.[6]
corresponds to no correlation (between points) in the typical statistical sense.[6]
Examples
Poisson point process
For a general Poisson point process with intensity measure 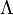 the
the  -th factorial moment measure is given by the expression:[3]
-th factorial moment measure is given by the expression:[3]
where 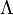 is the intensity measure or first moment measure of
is the intensity measure or first moment measure of 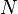 , which for some Borel set
, which for some Borel set 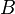 is given by:
is given by:
For a homogeneous Poisson point process the  -th factorial moment measure is simply:[2]
-th factorial moment measure is simply:[2]
where 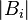 is the length, area, or volume (or more generally, the Lebesgue measure) of
is the length, area, or volume (or more generally, the Lebesgue measure) of 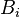 . Furthermore, the
. Furthermore, the  -th factorial moment density is:[3]
-th factorial moment density is:[3]
The pair-correlation function of the homogeneous Poisson point process is simply
which reflects the lack of interaction between points of this point process.
Factorial moment expansion
The expectations of general functionals of simple point processes, provided some certain mathematical conditions, have (possibly infinite) expansions or series consisting of the corresponding factorial moment measures.[11][12] In comparison to the Taylor series, which consists of a series of derivatives of some function, the nth factorial moment measure plays the roll as that of the n th derivative the Taylor series. In other words, given a general functional f of some simple point process, then this Taylor-like theorem for non-Poisson point processes means an expansion exists for the expectation of the function E, provided some mathematical condition is satisfied, which ensures convergence of the expansion.
See also
References
- 1 2 3 4 D. J. Daley and D. Vere-Jones. An introduction to the theory of point processes. Vol. I. Probability and its Applications (New York). Springer, New York, second edition, 2003.
- 1 2 3 4 5 6 7 Baccelli, F. O. (2009). "Stochastic Geometry and Wireless Networks: Volume I Theory". Foundations and Trends® in Networking 3 (3–4): 249–449. doi:10.1561/1300000006.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 D. Stoyan, W. S. Kendall, J. Mecke, and L. Ruschendorf. Stochastic geometry and its applications, volume 2. Wiley Chichester, 1995.
- ↑ Hough, J Ben, Krishnapur, Manjunath, Peres, Yuval, Vir{\'a}g, B{\'a}lint (2006). "Determinantal processes and independence". Probability Surveys 3: 206–229. doi:10.1214/154957806000000078.
- ↑ K. Handa. The two-parameter {Poisson-Dirichlet} point process. Bernoulli, 15(4):1082–1116, 2009.
- 1 2 3 4 5 A. Baddeley, I. B{\'a}r{\'a}ny, and R. Schneider. Spatial point processes and their applications. Stochastic Geometry: Lectures given at the CIME Summer School held in Martina Franca, Italy, September 13–18, 2004, pages 1–75, 2007.
- 1 2 3 D. J. Daley and D. Vere-Jones. An introduction to the theory of point processes. Vol. {II}. Probability and its Applications (New York). Springer, New York, second edition, 2008
- 1 2 3 Moller, J.; Plenge Waagepetersen, R. (2003). "Statistical Inference and Simulation for Spatial Point Processes". C&H/CRC Monographs on Statistics & Applied Probability 100. doi:10.1201/9780203496930. ISBN 978-1-58488-265-7.
- 1 2 F. Baccelli and B. Błaszczyszyn. Stochastic Geometry and Wireless Networks, Volume II – Applications, volume 4, No 1–2 of Foundations and Trends in Networking. NoW Publishers, 2009.
- ↑ J. F. C. Kingman. Poisson processes, volume 3. Oxford university press, 1992.
- ↑ B. Blaszczyszyn. Factorial-moment expansion for stochastic systems. Stoch. Proc. Appl., 56:321–335, 1995.
- ↑ D. P. Kroese and V. Schmidt. Light-traffic analysis for queues with spatially distributed arrivals. Mathematics of Operations Research, 21(1):pp. 135–157, 1996.
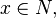
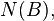
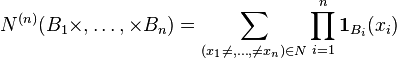
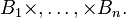
![M^{(n)}(B_1\times,\dots,\times B_n)=E [{N}^{(n)}(B_1\times,\dots,\times B_n)],](../I/m/22ed5927d59636c701f3e6624eafecec.png)
![\int_{\textbf{R}^{n d}}f(x_1,\dots,x_n) M^{(n)}(dx_1,\dots,dx_n)=E \left[ \sum_{(x_1\neq,\dots,\neq x_n)\in {N} } f(x_1,\dots,x_n) \right],](../I/m/b98658ca81d718c1ba56b6ce292a3def.png)
![M^{(1)}(B)=M^1(B)=E [{N}(B)],](../I/m/5aa0406462a3f8f0681dbeb8bef00826.png)
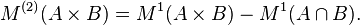
![M^{(n)}(B\times,\dots,\times B)=E [{N}(B)({N}(B)-1)\dots ({N}(B)-n+1)],](../I/m/0e28fd11c26ab351d79cf15f5095d29e.png)
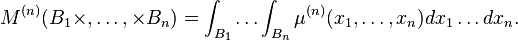
![E \left[ \sum_{(x_1\neq,\dots,\neq x_n)\in {N} } f(x_1,\dots,x_n) \right]= \int_{\textbf{R}^{n d}} f(x_1,\dots,x_n) \mu^{(n)}(x_1,\dots,x_n) dx_1\dots dx_n,](../I/m/d558a8783f50731068c0a56e4de6f11b.png)
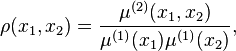
![M^{(n)}(B_1\times,\dots,\times B_n)=\prod_{i=1}^n[\Lambda(B_i)],](../I/m/70eeae758bf8ecefcce0681b596bfa0f.png)
![\Lambda(B)=M^1(B)=E[{N}(B)].](../I/m/b8c7fe2e47f27f7f52b3e1b5a9318b27.png)