Factorial moment
In probability theory, the factorial moment is a mathematical quantity defined as the expectation or average of the falling factorial of a random variable. Factorial moments are useful for studying non-negative integer-valued random variables.[1] and arise in the use of probability-generating functions to derive the moments of discrete random variables.
Factorial moments serve as analytic tools in the mathematical field of combinatorics, which is the study of discrete mathematical structures.[2]
Definition
For a natural number r, the r-th factorial moment of a probability distribution on the real or complex numbers, or, in other words, a random variable X with that probability distribution, is[3]
where the E is the expectation (operator) and
is the falling factorial, which gives rise to the name, although the notation (x)r varies depending on the mathematical field. [lower-alpha 1] Of course, the definition requires that the expectation is meaningful, which is the case if (X)r ≥ 0 or E[|(X)r|] < ∞.
Examples
Poisson distribution
If a random variable X has a Poisson distribution with parameter or expected value λ ≥ 0, then the factorial moments of X are
The Poisson distribution has a factorial moments with straightforward form compared to its moments, which involve Stirling numbers of the second kind.
Binomial distribution
If a random variable X has a binomial distribution with success probability p ∈ [0,1] and number of trials n, then the factorial moments of X are[5]
where ! denotes the factorial of a non-negative integer. For all r > n, the factorial moments are zero.
Hypergeometric distribution
If a random variable X has a hypergeometric distribution with population size N, number of success states K ∈ {0,...,N} in the population, and draws n ∈ {0,...,N}, then the factorial moments of X are [5]
For all larger r, the factorial moments are zero.
Beta-binomial distribution
If a random variable X has a beta-binomial distribution with parameters α > 0, β > 0, and number of trials n, then the factorial moments of X are
where B denotes the beta function. For all r > n, the factorial moments are zero.
Calculation of moments
In the examples above, the n-th moment of the random variable X can be calculated by the formula
where the curly braces denote Stirling numbers of the second kind.
See also
Notes
- ↑ Confusingly, this same notation, the Pochhammer symbol (x)r, is used, especially in the theory of special functions, to denote the rising factorial x(x + 1)(x + 2) ... (x + r − 1);.[4] whereas the present notation is used more often in combinatorics.
References
- ↑ D. J. Daley and D. Vere-Jones. An introduction to the theory of point processes. Vol. I. Probability and its Applications (New York). Springer, New York, second edition, 2003.
- ↑ Riordan, John (1958). Introduction to Combinatorial Analysis. Dover.
- ↑ Riordan, John (1958). Introduction to Combinatorial Analysis. Dover. p. 30.
- ↑ NIST Digital Library of Mathematical Functions. Retrieved 9 November 2013.
- 1 2 Potts, RB (1953). "Note on the factorial moments of standard distributions". Australian Journal of Physics (CSIRO) 6 (4): 498–499. doi:10.1071/ph530498.
![\operatorname{E}\bigl[(X)_r\bigr] = \operatorname{E}\bigl[ X(X-1)(X-2)\cdots(X-r+1)\bigr],](../I/m/2e7aedab23285122b7ee30095145ebf2.png)
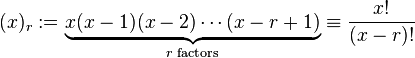
![\operatorname{E}\bigl[(X)_r\bigr] =\lambda^r,\qquad r\in\mathbb{N}_0.](../I/m/f861e158d5c334dc33c0ae56f32924ee.png)
![\operatorname{E}\bigl[(X)_r\bigr] = \frac{n!}{(n-r)!} p^r,\qquad r\in\{0,1,\ldots,n\},](../I/m/0d86c69040e098abeafcbc4793e9e78a.png)
![\operatorname{E}\bigl[(X)_r\bigr] = \frac{K!}{(K-r)!} \frac{n!}{(n-r)!} \frac{(N-r)!}{N!},\qquad r\in\{0,1,\ldots,\min\{n,K\}\}.](../I/m/d8b26b3f04f36abba83dfd9c6f9080a3.png)
![\operatorname{E}\bigl[(X)_r\bigr] = \frac{n!}{(n-r)!}\frac{B(\alpha+r,\beta)}{B(\alpha,\beta)},\qquad r\in\{0,1,\ldots,n\},](../I/m/7a35f8557a7fef71e502212b6427dd83.png)
![\operatorname{E}\bigl[X^n\bigr]=\sum_{r=0}^n\biggl\{{n\atop r}\biggr\}\operatorname{E}\bigl[(X)_r\bigr],\qquad n\in\mathbb{N}_0,](../I/m/34e2c74cb443035871d71dafbf7578e0.png)