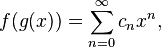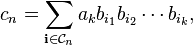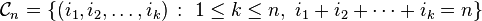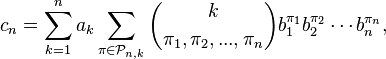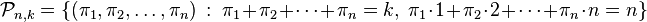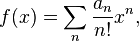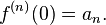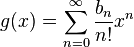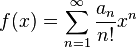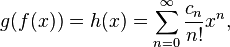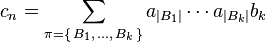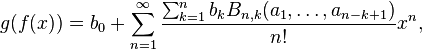Faà di Bruno's formula
| Part of a series of articles about | ||||||
| Calculus | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
Specialized |
||||||
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after Francesco Faà di Bruno (1855, 1857), though he was not the first to state or prove the formula. In 1800, more than 50 years before Faà di Bruno, the French mathematician Louis François Antoine Arbogast stated the formula in a calculus textbook,[1] considered the first published reference on the subject.[2]
Perhaps the most well-known form of Faà di Bruno's formula says that
where the sum is over all n-tuples of nonnegative integers (m1, …, mn) satisfying the constraint
Sometimes, to give it a memorable pattern, it is written in a way in which the coefficients that have the combinatorial interpretation discussed below are less explicit:
Combining the terms with the same value of m1 + m2 + ... + mn = k and noticing that m j has to be zero for j > n − k + 1 leads to a somewhat simpler formula expressed in terms of Bell polynomials Bn,k(x1,...,xn−k+1):
Combinatorial form
The formula has a "combinatorial" form:
where
- π runs through the set Π of all partitions of the set { 1, ..., n },
- "B ∈ π" means the variable B runs through the list of all of the "blocks" of the partition π, and
- |A| denotes the cardinality of the set A (so that |π| is the number of blocks in the partition π and |B| is the size of the block B).
Explanation via an example
The combinatorial form may initially seem forbidding, so let us examine a concrete case, and see what the pattern is:
The pattern is
The factor 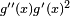 corresponds to the partition 2 + 1 + 1 of the integer 4, in the obvious way. The factor
corresponds to the partition 2 + 1 + 1 of the integer 4, in the obvious way. The factor 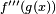 that goes with it corresponds to the fact that there are three summands in that partition. The coefficient 6 that goes with those factors corresponds to the fact that there are exactly six partitions of a set of four members that break it into one part of size 2 and two parts of size 1.
that goes with it corresponds to the fact that there are three summands in that partition. The coefficient 6 that goes with those factors corresponds to the fact that there are exactly six partitions of a set of four members that break it into one part of size 2 and two parts of size 1.
Similarly, the factor 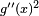 in the third line corresponds to the partition 2 + 2 of the integer 4, (4, because we are finding the fourth derivative), while
in the third line corresponds to the partition 2 + 2 of the integer 4, (4, because we are finding the fourth derivative), while 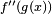 corresponds to the fact that there are two summands (2 + 2) in that partition. The coefficient 3 corresponds to the fact that there are
corresponds to the fact that there are two summands (2 + 2) in that partition. The coefficient 3 corresponds to the fact that there are 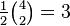 ways of partitioning 4 objects into groups of 2. The same concept applies to the others.
ways of partitioning 4 objects into groups of 2. The same concept applies to the others.
A memorizable scheme is as follows:
Combinatorics of the Faà di Bruno coefficients
These partition-counting Faà di Bruno coefficients have a "closed-form" expression. The number of partitions of a set of size n corresponding to the integer partition
of the integer n is equal to
These coefficients also arise in the Bell polynomials, which are relevant to the study of cumulants.
Variations
Multivariate version
Let y = g(x1, ..., xn). Then the following identity holds regardless of whether the n variables are all distinct, or all identical, or partitioned into several distinguishable classes of indistinguishable variables (if it seems opaque, see the very concrete example below):[3]
where (as above)
- π runs through the set Π of all partitions of the set { 1, ..., n },
- "B ∈ π" means the variable B runs through the list of all of the "blocks" of the partition π, and
- |A| denotes the cardinality of the set A (so that |π| is the number of blocks in the partition π and |B| is the size of the block B).
A further generalization, due to Tsoy-Wo Ma, considers the case where y is a vector-valued variable.[4] The general form, for variational calculus (Gâteaux differentials are the most general form of differential), was derived in 2012.[5]
- Example
The five terms in the following expression correspond in the obvious way to the five partitions of the set { 1, 2, 3 }, and in each case the order of the derivative of f is the number of parts in the partition:
If the three variables are indistinguishable from each other, then three of the five terms above are also indistinguishable from each other, and then we have the classic one-variable formula.
Formal power series version
Suppose 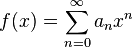 and
and 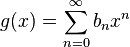 are formal power series and
are formal power series and 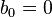 .
.
Then the composition  is again a formal power series,
is again a formal power series,
and the coefficient cn, for n ≥ 1, can be expressed as a sum over compositions of n or as an equivalent sum over partitions of n :
where
is the set of compositions of n with k denoting the number of parts,
or
where
is the set of partitions of n into k parts, in frequency-of-parts form.
The first form is obtained by picking out the coefficient of xn
in 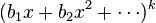 "by inspection", and the second form
is then obtained by collecting like terms, or alternatively, by applying the multinomial theorem.
"by inspection", and the second form
is then obtained by collecting like terms, or alternatively, by applying the multinomial theorem.
The special case f(x) = ex, g(x) = ∑n ≥ 1 an /n! xn gives the exponential formula. The special case f(x) = 1/(1 − x), g(x) = ∑n ≥ 1 (−an) xn' gives an expression for the reciprocal of the formal power series ∑n ≥ 0 an xn in the case a0 = 1.
Stanley [6] gives a version for exponential power series. In the formal power series
we have the nth derivative at 0:
This should not be construed as the value of a function, since these series are purely formal; there is no such thing as convergence or divergence in this context.
If
and
and
then the coefficient cn (which would be the nth derivative of h evaluated at 0 if we were dealing with convergent series rather than formal power series) is given by
where π runs through the set of all partitions of the set { 1, ..., n } and B1, ..., Bk are the blocks of the partition π, and | Bj | is the number of members of the jth block, for j = 1, ..., k.
This version of the formula is particularly well suited to the purposes of combinatorics.
We can also write with respect to the notation above
where Bn,k(a1,...,an−k+1) are Bell polynomials.
A special case
If f(x) = ex then all of the derivatives of f are the same, and are a factor common to every term. In case g(x) is a cumulant-generating function, then f(g(x)) is a moment-generating function, and the polynomial in various derivatives of g is the polynomial that expresses the moments as functions of the cumulants.
Notes
- ↑ Arbogast, L.F.A. (1800). Du calcul des derivations. Strasbourg: Levrault.
- ↑ Craik, A.D.D. (2005). "Prehistory of Faà di Bruno's Formula". American Mathematical Monthly (Mathematical Association of America) 112 (2): 217–234. doi:10.2307/30037410. JSTOR 30037410.
- ↑ Hardy, Michael (2006). "Combinatorics of Partial Derivatives". Electronic Journal of Combinatorics 13 (1): R1.
- ↑ Tsoy Wo Ma (2009). "Higher Chain Formula proved by Combinatorics". Electronic Journal of Combinatorics 16 (1): N21.
- ↑ Clark, Daniel; Houssineau, Jeremie (2012). "Hierarchical stochastic population processes". arXiv:1202.0264.
- ↑ See the "compositional formula" in Chapter 5 of Stanley, Richard P. (1999) [1997]. Enumerative Combinatorics. Cambridge University Press. ISBN 0-521-55309-1.
References
Historical surveys and essays
- Brigaglia, Aldo (2004), "L'Opera Matematica", in Giacardi, Livia, Francesco Faà di Bruno. Ricerca scientifica insegnamento e divulgazione, Studi e fonti per la storia dell'Università di Torino (in Italian) XII, Torino: Deputazione Subalpina di Storia Patria, pp. 111–172. "The mathematical work" is an essay on the mathematical activity, describing both his research and teaching, of Francesco Faà di Bruno.
- Craik, Alex D. D. (February 2005), "Prehistory of Faà di Bruno's Formula", American Mathematical Monthly 112 (2): 217–234, doi:10.2307/30037410, JSTOR 30037410, MR 2121322, Zbl 1088.01008.
- Johnson, Warren P. (March 2002), "The Curious History of Faà di Bruno's Formula" (PDF), American Mathematical Monthly 109 (3): 217–234, doi:10.2307/2695352, JSTOR 2695352, MR 1903577, Zbl 1024.01010.
Research works
- Arbogast, L. F. A. (1800), Du calcul des derivations (in French), Strasbourg: Levrault, pp. xxiii+404, Entirely freely available from Google books.
- Faà di Bruno, F. (1855), "Sullo sviluppo delle funzioni" [On the development of the functions], Annali di Scienze Matematiche e Fisiche (in Italian) 6: 479–480, LCCN 06036680. Entirely freely available from Google books. A well-known paper where Francesco Faà di Bruno presents the two versions of the formula that now bears his name, published in the journal founded by Barnaba Tortolini.
- Faà di Bruno, F. (1857), "Note sur une nouvelle formule de calcul differentiel", The Quarterly Journal of Pure and Applied Mathematics (in French) 1: 359–360. Entirely freely available from Google books.
- Faà di Bruno, Francesco (1859), Théorie générale de l'élimination (in French), Paris: Leiber et Faraguet, pp. x+224. Entirely freely available from Google books.
- Fraenkel, L. E. (1978), "Formulae for high derivatives of composite functions", Mathematical Proceedings of the Cambridge Philosophical Society 83 (2): 159–165, doi:10.1017/S0305004100054402, MR 0486377, Zbl 0388.46032
- Krantz, Steven G.; Parks, Harold R. (2002), A Primer of Real Analytic Functions, Birkhäuser Advanced Texts - Basler Lehrbücher (Second ed.), Boston: Birkhäuser Verlag, pp. xiv+205, ISBN 0-8176-4264-1, MR 1916029, Zbl 1015.26030
- Porteous, Ian R. (2001), "Paragraph 4.3: Faà di Bruno's formula", Geometric Differentiation (Second ed.), Cambridge: Cambridge University Press, pp. 83–85, ISBN 0-521-00264-8, MR 1871900, Zbl 1013.53001.
- T. A., (Tiburce Abadie, J. F. C.) (1850), "Sur la différentiation des fonctions de fonctions", Nouvelles annales de mathématiques, journal des candidats aux écoles polytechnique et normale, Série 1, (in French) 9: 119–125, available at NUMDAM. This paper, according to Johnson (2002, p. 228) is one of the precursors of Faà di Bruno 1855: note that the author signs only as "T.A.", and the attribution to J. F. C. Tiburce Abadie is due again to Johnson.
- A., (Tiburce Abadie, J. F. C.) (1852), "Sur la différentiation des fonctions de fonctions. Séries de Burmann, de Lagrange, de Wronski", Nouvelles annales de mathématiques, journal des candidats aux écoles polytechnique et normale, Série 1, (in French) 11: 376–383, available at NUMDAM. This paper, according to Johnson (2002, p. 228) is one of the precursors of Faà di Bruno 1855: note that the author signs only as "A.", and the attribution to J. F. C. Tiburce Abadie is due again to Johnson.
External links
- Weisstein, Eric W., "Faa di Bruno's Formula", MathWorld.
- An intuitive presentation of Faà di Bruno's formula, with examples
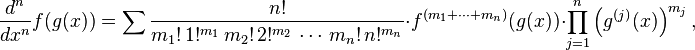
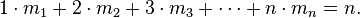
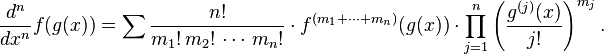
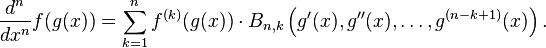
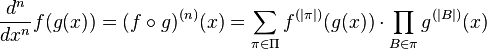
![\begin{align}
(f\circ g)''''(x)
& = f''''(g(x))g'(x)^4
+ 6f'''(g(x))g''(x)g'(x)^2 \\[8pt]
& {} \quad+\; 3f''(g(x))g''(x)^2
+ 4f''(g(x))g'''(x)g'(x) \\[8pt]
& {} \quad+\; f'(g(x))g''''(x).
\end{align}](../I/m/ba2b1915b2925a012dc82d62e884e967.png)
![\begin{align}
g'(x)^4
& & \leftrightarrow & & 1+1+1+1
& & \leftrightarrow & & f''''(g(x))
& & \leftrightarrow & & 1
\\[12pt]
g''(x)g'(x)^2
& & \leftrightarrow & & 2+1+1
& & \leftrightarrow & & f'''(g(x))
& & \leftrightarrow & & 6
\\[12pt]
g''(x)^2
& & \leftrightarrow & & 2+2
& & \leftrightarrow & & f''(g(x))
& & \leftrightarrow & & 3
\\[12pt]
g'''(x)g'(x)
& & \leftrightarrow & & 3+1
& & \leftrightarrow & & f''(g(x))
& & \leftrightarrow & & 4
\\[12pt]
g''''(x)
& & \leftrightarrow & & 4
& & \leftrightarrow & & f'(g(x))
& & \leftrightarrow & & 1.
\end{align}](../I/m/af11c69a5df7c4e52e89cd3650c2d8a7.png)
![\begin{align} & \frac{D^1(f\circ{}g)}{1!} & = \left(f^{(1)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!} }{1!} \\[8pt]
& \frac{D^2(f\circ g)}{2!} & = \left(f^{(1)}\circ{}g\right)\frac{\frac{g^{(2)} }{2!} }{1!} & {} + \left(f^{(2)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!} }{2!} \\[8pt]
& \frac{D^3(f\circ g)}{3!} & = \left(f^{(1)}\circ{}g\right)\frac{\frac{g^{(3)} }{3!} }{1!} & {} + \left(f^{(2)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!} }{1!}\frac{\frac{g^{(2)} }{2!} }{1!} & {} + \left(f^{(3)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!} }{3!} \\[8pt]
& \frac{D^4(f\circ g)}{4!} & = \left(f^{(1)}\circ{}g\right)\frac{\frac{g^{(4)} }{4!} }{1!} & {} + \left(f^{(2)}\circ{}g\right)\left(\frac{\frac{g^{(1)} }{1!} }{1!}\frac{\frac{g^{(3)} }{3!} }{1!}+\frac{\frac{g^{(2)} }{2!}\frac{g^{(2)} }{2!} }{2!}\right) & {} + \left(f^{(3)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!} }{2!}\frac{\frac{g^{(2)} }{2!} }{1!} & {} + \left(f^{(4)}\circ{}g\right)\frac{\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!}\frac{g^{(1)} }{1!} }{4!}
\end{align}](../I/m/f3b9c3ea61af693a4ec12d2031210339.png)
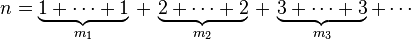
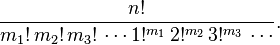
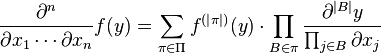
![\begin{align}
{\partial^3 \over \partial x_1\, \partial x_2\, \partial x_3}f(y)
& = f'(y){\partial^3 y \over \partial x_1\, \partial x_2\, \partial x_3} \\[10pt]
& {} + f''(y) \left( {\partial y \over \partial x_1}
\cdot{\partial^2 y \over \partial x_2\, \partial x_3}
+{\partial y \over \partial x_2}
\cdot{\partial^2 y \over \partial x_1\, \partial x_3}
+ {\partial y \over \partial x_3}
\cdot{\partial^2 y \over \partial x_1\, \partial x_2}\right) \\[10pt]
& {} + f'''(y) {\partial y \over \partial x_1}
\cdot{\partial y \over \partial x_2}
\cdot{\partial y \over \partial x_3}.
\end{align}](../I/m/1a0aa4f6782b45104bb5a031fd559635.png)