Felix Hausdorff

Felix Hausdorff
Born (1868-11-08)November 8, 1868
Breslau, Kingdom of Prussia
Died January 26, 1942(1942-01-26) (aged 73)
Bonn, Germany
Nationality German
Fields Mathematics
Institutions University of Bonn, University of Greifswald, University of Leipzig
Alma mater University of Leipzig
Thesis Zur Theorie der astronomischen Strahlenbrechung (1891)
Doctoral advisor Heinrich Bruns
Adolph Mayer
Doctoral students Karl Bögel
Franz Hallenbach
Gustav Steinbach
Known for Hausdorff measure
Hausdorff dimension
Hausdorff space
Hausdorff maximal principle
Hausdorff distance
Hausdorff paradox
Hausdorff moment problem
Hausdorff-Young inequality

Felix Hausdorff (November 8, 1868 – January 26, 1942) was a German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.

Life

Childhood and youth

Hausdorff's father, the Jewish merchant Louis Hausdorff (1843-1896), moved in the autumn of 1870 with his young family to Leipzig and worked over time at various companies, including a linen-and cotton goods factory. He was an educated man and had become a Morenu at the age of 14. There are several treatises from his pen, including a long work on the Aramaic translations of the Bible from the perspective of Talmudic law.

Hausdorff's mother, Hedwig (1848-1902), who is also referred to in various documents as Johanna, came from the Jewish Tietz family. From another branch of this family came Hermann Tietz, founder of the first department store, and later co-owner of the department store chain called "Hermann Tietz". During the period of Nazi dictatorship the name was "Aryanised" to Hertie.

From 1878 to Felix Hausdorff attended the Nicolai School in Leipzig, a facility that had a reputation as a hotbed of humanistic education. He was an excellent student, class leader for many years and often recited self-written Latin or German poems at school celebrations. In his graduation in 1887 (with two Oberprimen), he was the only one who reached the highest grade.

The choice of subject was not easy for Hausdorff. Magda Dierkesmann, who was often a guest in the home of Hausdorff as a student in Bonn in the years 1926-1932, reported in 1967 that:

"His versatile musical talent was so great that only the insistence of his father made him give up his plan to study music and become a composer."

The decision was made to study the sciences in high school.

Degree, doctorate and habilitation

From summer term 1887 to summer semester 1891 Hausdorff studied mathematics and astronomy, mainly in his native city of Leipzig, interrupted by one semester in Freiburg (summer semester 1888) and Berlin (winter semester 1888/1889). The surviving testimony of other students show him as extremely versatile interested young man, who, in addition to the mathematical and astronomical lectures, attended lectures in physics, chemistry and geography, and also lectures on philosophy and history of philosophy as well as on issues of language, literature and social sciences. In Leipzig he heard lectures on the history of music from musicologist Paul. His early love of music lasted a lifetime; in Hausdorff's house there were impressive musical evenings with the landlord at the piano, according to witness statements made by various participants. Even as a student in Leipzig, he was an admirer and connoisseur of the music of Richard Wagner.

In later semesters of his studies, Hausdorff was close to Heinrich Bruns (1848-1919). Bruns was professor of astronomy and director of the observatory at the University of Leipzig. Under him, Hausdorff graduated in 1891 with a work on the theory of astronomical refraction of light in the atmosphere. Two publications on the same subject followed, and in 1895 his habilitation also followed with a thesis on the absorbance of light in the atmosphere. These early astronomical work Hausdorff have - despite their excellent mathematical working through - not gained importance. Firstly, the underlying idea of Brunswick has not proved viable (there were needs for refraction observations near the astronomical horizon, which - as Julius Bauschinger could show a little later - in principle can not be obtained with the required accuracy). On the other hand, the progress in the direct measurement of atmospheric data (balloon ascents) has soon made the painstaking accuracy of this data from refraction observations unnecessary. In the time between PhD and habilitation Hausdorff completed the yearlong-volunteer military requirement and worked for two years as a computer at the observatory in Leipzig .

Docent in Leipzig

With his habilitation, Hausdorff became a lecturer at the University of Leipzig and began an extensive teaching in a variety of mathematical areas. In addition to teaching and research in mathematics, he went with his literary and philosophical inclinations. A man of varied interests, educated, highly sensitive and sophisticated in thinking, feeling and experiencing, he frequented in his Leipzig period with a number of famous writers, artists and publishers such as Hermann Conradi, Richard Dehmel, Otto Erich Hartleben, Gustav Kirstein, Max Klinger, Max Reger and Frank Wedekind. The years 1897 to about 1904 mark the high point of his literary and philosophical creativity, during which time 18 of his 22 pseudonymous works were published, including a book of poetry, a play, an epistemological book and a volume of aphorisms .

Hausdorff married Charlotte Goldschmidt in 1899, daughter of Jewish doctor Siegismund Goldschmidt. Her stepmother was the famous suffragist and preschool teacher Henriette Goldschmidt . In 1900 Hausdorff's only child, daughter Lenore (Nora), was born, who survived the era of National Socialism and died very old in 1991 in Bonn.

First professorship

In December 1901 Hausdorff was appointed as adjunct associate professor at the University of Leipzig. The often repeated assertion that Hausdorff got a call from Göttingen and rejected it can not be verified and is probably wrong. When applying in Leipzig, Dean Kirchner had been led to very positive vote of his colleagues, written by Heinrich Bruns, still accompanied by the following words:

"The faculty, however, considers itself obliged to report to the Royal Ministry, that the above application in the second November of this year faculty meeting had taken place was not accepted by all, but with 22 votes to 7. The minority was opposed, because Dr. Hausdorff is of the Mosaic faith."[1]}

This quote emphasizes the undisguised anti-Semitism present, which especially took a sharp upturn after the Gründerkrach in 1873 throughout the German Reich. Leipzig was a center of anti-Semitic movement, especially among the student body. This may well be the reason that Hausdorff did not feel at ease at Leipzig. Another reason was perhaps the stresses due to the hierarchical posturing of the Leipzig professors.

After his habilitation, Hausdorff wrote another work on optics, on non-Euclidean geometry, and on hypercomplex number systems, as well as two papers on probability theory. However, his main area of work soon became set theory, especially the theory of ordered sets. It was initially a philosophical interest, which led him around 1897 to study Georg Cantor's work. Already, in the summer semester of 1901, Hausdorff gave a lecture on set theory. This was one of the first lectures on set theory at all; Ernst Zermelo's lectures in Göttingen College during the winter semester of 1900/1901 was a little earlier. That year, he published his first paper on order types in which he examined a generalization of well-orderings called graded order types, where a linear order is graded if no two of its segments share the same order type. He generalized a result which said the collection of countable order types has the cardinality of the continuum and showed that the collection of all graded types of an idempotent cardinality m has a cardinality of 2m.[2]

For the summer semester 1910 Hausdorff was appointed as professor to the University of Bonn. In Bonn, he began a lecture on set theory, which he repeated in the summer semester 1912, substantially revised and expanded.

In the summer of 1912 he also began work on his magnum opus, the book "Basics of set theory". It was completed in Greifswald, where Hausdorff had been appointed for the summer semester as full professor in 1913, and was released in April 1914.

The University of Greifswald was the smallest of the Prussian universities. Also, the mathematical institute was small; in the summer semester 1916 and winter semester 1916/17 Hausdorff was the only mathematician in Greifswald. This brought with it that he was almost fully occupied in teaching the basic courses. It was a substantial improvement of his academic situation when Hausdorff was appointed in 1921 to Bonn. Here he could develop a thematically wide-spanned teaching and always lecture on the latest research. He gave a particularly noteworthy lecture on probability theory (NL Hausdorff: Capsule 21: Fasz 64) in the summer semester 1923, in which he grounded this theory in measure-theoretic axiomatic theory, and this occurred ten years before AT Kolmogorov's "Basic concepts of probability theory" (reprinted in full in the collected works, Volume V). In Bonn, Hausdorff had Eduard Study, and later with Otto Toeplitz, outstanding mathematicians as well as colleagues and friends.

Hausdorff under the Nazi dictatorship

The National Socialist party's state doctrine established Anti-Semitism and the seizure of power. Hausdorff was not initially concerned by the "Law for the Restoration of the Professional Civil Service", adopted in 1933, because he had been a German official since before 1914. However, he was not completely spared, as one of his lectures was interrupted by Nazi students. He stopped his 1934/1935 winter semester Calculus III course from 20 November on. During that time, there was a working session of the National Socialist German Student Union (NSDStB) at the University of Bonn, which chose "Race and Ethnicity" as their theme for the semester. The assumption is that this event is related to the cancellation of Hausdorff's class, because otherwise he never, in his long career as a university teacher, stopped a class.

In March 31, 1935, after some going back and forth, Hausdorff was finally given emeritus status. No words of thanks were given for 40 years of successful work in the German higher education system. He worked tirelessly and published, in addition to the expanded edition of his work on set theory, seven works on topology and descriptive set theory, all published in Polish magazines: one in Studia Mathematica, the others in Fundamenta Mathematicae.

His Nachlass shows that Hausdorff was still working mathematically at these increasingly difficult times and following current developments of interest. He was selflessly supported at this time by Erich Bessel-Hagen, a loyal friend to the Hausdorff family who obtained books and magazines from the Library of the Institute, which Hausdorff was no longer allowed to enter as a Jew.

About the humiliations to which Hausdorff and his family especially were exposed to after Kristallnacht in 1938, much is known and from many different sources, such as from the letters of Bessel-Hagen.[3]

In vain, Hausdorff asked the mathematician Richard Courant in 1939 for a research fellowship to be able to emigrate into the USA.

The first page of his farewell letter to Hans Wollstein

Mid-1941, the Bonn Jews began to be deported to the Monastery "To Perpetual Adoration" in Endenich, from which the nuns had been expelled. The transports to the death camps in the East occurred later. After Felix Hausdorff, his wife and his wife's sister, Edith Pappenheim (who was living with them) were ordered in January 1942 to move to the Endenich camp, they committed suicide on 26 January 1942 by taking an overdose of veronal. Their final resting place is located on the Poppelsdorfer cemetery in Bonn. Between their placement in temporary camps and his suicide, he gave his handwritten Nachlass to the Egyptologist and presbyter Hans Bonnet, who saved as much of them as possible, despite the destruction of his house by a bomb.

Some of his fellow Jews may have had illusions about the camp Endenich, but not Hausdorff. E. Neuenschwander discovered in the estate of Bessel-Hagen the farewell letter that Hausdorff wrote to his Jewish lawyer Hans Wollstein.[4][5] Here is the beginning and end of the letter:

Hausdorff's gravestone in Bonn-Poppelsdorf

"Dear Friend Wollstein! If you receive these lines, we (three) have solved the problem in a different manner - in the manner of which you have constantly tried to dissuade us. The feeling of security that you have predicted for us once we would overcome the difficulties of the move, is still eluding us; on the contrary, Endenich may not even be the end! What has happened in recent months against the Jews evokes justified fear that they will not let us live to see a more bearable situation."

After thanking friends and, in great composure, expressing his last wishes regarding his funeral and his will, Hausdorff writes:

"I am sorry that we cause you yet more effort beyond death, and I am convinced that you are doing what you can do (which perhaps is not very much). Forgive us our desertion! We wish you and all our friends to experience better times.

Your truly devoted

Felix Hausdorff "

Unfortunately, this desire was not fulfilled. Hausdorff's lawyer Wollstein was murdered in Auschwitz.

Hausdorffstraße (Bonn)

Hausdorff's library was sold by his son-in-law and sole heir, Arthur König. The handwritten Nachlass was adopted by a family friend, the Bonn Egyptologist Hans Bonnet, for storage. It is now in the University and State Library of Bonn. The Nachlass is cataloged.[6]

Work and reception

Hausdorff as philosopher and writer (Paul Mongré)

His volume of aphorisms in 1897 was the first published work of Hausdorff under the pseudonym Paul Mongré. It is entitled Sant' Ilario. Thoughts from the landscape of Zarathustra. The subtitle of Sant 'Ilario "Thoughts from the landscape Zarathustra" plays first on the fact that Hausdorff had completed his book during a recovery stay on the Ligurian coast to Genoa and that Friedrich Nietzsche in this same area wrote the first two parts of Thus Spoke Zarathustra: he also alludes to the spiritual closeness to Nietzsche. In an article on Sant 'Ilario in the weekly paper Die Zukunft, Hausdorff acknowledged expressis verbis to Nietzsche.

Hausdorff was not trying to copy or even exceed Nietzsche. "Of Nietzsche imitation no trace," says a contemporary review. He follows Nietzsche in an attempt to liberate individual thinking, to take the liberty of questioning outdated standards. Hausdorff maintained critical distance to the late works of Nietzsche. In his essay on the book The Will to Power compiled from notes left in the Nietzsche Archive he says:

"In Nietzsche glows a fanatic. His morality of breeding, erected on our present biological and physiological foundations of knowledge: that could be a world historical scandal against which the Inquisition and witch trials fade into harmless aberrations ".

His critical standard he took from Nietzsche himself,

"From the kind, modest, understanding Nietzsche and from the free spirit of the cool, dogma-free, unsystematic skeptic Nietzsche [...]"

In 1898 appeared- also under the pseudonym Paul Mongré - Hausdorff's epistemological experiment Chaos in cosmic selection. The critique of metaphysics put forward in this book had its starting point in Hausdorff's confrontation with Nietzsche's idea of eternal recurrence. It ultimately gets to destroying any kind of metaphysics. Of the world itself, from the transcendent world core - as Hausdorff expressed - we know nothing and we know nothing. We must assume "the world itself" as undetermined and undeterminable, as a mere chaos. The world of our experience, our cosmos is the result of the selection, the selection that we have always instinctively made according to our possibilities of understanding and make more. From that chaos would also be seen other orders, other Kosmoi, conceivably. At any rate, from the world of our cosmos you can not conclude the existence of a transcendent world.

In 1904, in the magazine The New Rundschau, Hausdorff's play appeared, the one-act play The Doctor in his honor. It is a crude satire on the duel and on the traditional concepts of honor and nobility of the Prussian officer corps, which in the developing bourgeois society were increasingly anachronistic. The physician in his honor was Hausdorff's greatest literary success. In 1914-1918 there were numerous performances in more than thirty cities. Hausdorff later wrote an epilogue to the play, but it was not performed at that time. Only in 2006 did this epilogue have its premier at the annual meeting of the German Mathematical Society in Bonn.

Besides the works above mentioned Hausdorff wrote numerous essays that appeared in some of the leading literary magazines of the time, as well as a book of poems, Ecstasy (1900). Some of his poems were set to music by Austrian composer Joseph Marx.

Theory of ordered sets

Hausdorff's entry into a thorough study of ordered sets was prompted in part by Cantor's continuum problem: which place does the cardinal number 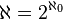\aleph = 2^{\aleph_0} take in the series 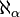\aleph_{\alpha}. In a letter to Hilbert on 29 September 1904, he speaks of this problem, "it has plagued almost like a monomania".[7] He saw in the set \mathrm{card} (T(\aleph_0)) = \aleph a new strategy to attack the problem. 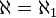Cantor had suspected \aleph = \aleph_1 suspected, but had only shown 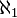\aleph \geq \aleph_1. \aleph_1 is the "number" of possible well-orderings of a countable set ; 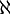\aleph had now emerged as the "number" of all possible orders of such an amount. It was natural, therefore, to study systems that are more special than general orders, but more general than well-orderings. Hausdorff did just that in his first volume of 1901 with the publication of theoretical studies of "graded sets". We know from the results of Kurt Gödel and Paul Cohen, that this strategy to solve the continuum problem is just as ineffectual as Cantor's strategy, which was aimed at generalizing the Cantor-Bendixson principle for closed sets to general uncountable sets.

In 1904 Hausdorff published the recursion named after him:

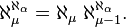
For each non-limit ordinal \mu we have \aleph_{\mu}^{\aleph_{\alpha}} = \aleph_{\mu} \; \aleph_{\mu -1}^{\aleph_{\alpha}}.

This formula was, together with the later notion of cofinality introduced by Hausdorff, the basis for all further results for Aleph exponentiation. Hausdorff' excellent knowledge of the problems of this type of sequence was also empowered by his efforts to uncover the error in Julius King's lecture at the International Congress of Mathematicians in 1904 in Heidelberg. There King had argued that the continuum can not be well-ordered, so its cardinality is no Aleph, and thus caused a great stir. The assertion that it was Hausdorff who clarified the mistake has a special weight because a false image was drawn in the historical literature for more than 50 years of the events in Heidelberg.[8]

In the years 1906-1909 Hausdorff did his fundamental work on ordered sets. Only a few points can be touched briefly. Of fundamental importance to the whole theory is the concept of cofinality that Hausdorff introduced. An ordinal is called regular if it is cofinal with any smaller ordinal; otherwise it is singular. Hausdorff's question whether there are regular numbers with index a limit ordinal, was the starting point for the theory of inaccessible cardinals. Hausdorff had already noticed that such numbers, if they exist, must be of "exorbitant size".[9]

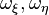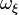Of fundamental importance is the following theorem of Hausdorff: for each unbounded ordered dense set A there are two uniquely determined regular initial numbers \omega_{\xi}, \omega_{\eta} so that A is cofinal with \omega_{\xi} and coinitial with 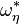\omega_{\eta}^* (* Denotes the inverse order). This theorem provides, for example, a technique to characterize elements and gaps in ordered sets. Thus Hausdorff utilized the gap characters and element characters introduced by him.

If W is a predetermined set of characters (element and gap characters), the question arises whether there are ordered sets whose character set is exactly W. One can easily find a necessary condition for W. Hausdorff was able to show that this condition is also sufficient. 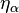For this one needs a rich reservoir of ordered sets; Hausdorff had created this with his theory of general products and powers.[10] In this reservoir such interesting structures are found as the Hausdorff \eta_{\alpha} normal-types, in connection with which Hausdorff first formulated the generalized continuum hypothesis. Hausdorff's 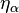\eta_{\alpha}-sets formed the starting point for the study of the important model theory of saturated structure.[11]

Hausdorff's general products and powers of cardinalities had led him to the concept of partially ordered set. The question of whether any ordered subset of a partially ordered set is contained in a maximal ordered subset was answered in the positive by Hausdorff using the well-ordering theorem. This is the Hausdorff maximal principle. It follows not only from the well-ordering theorem (or from the (equivalent to this) axiom of choice), but it is, as it turned out, even to the axiom of choice are equivalent.[12]

Already, in 1908, Arthur Moritz Schoenflies found in the second part of his report on set theory, that the newer theory of ordered sets (i.e., that which occurred after Cantor's extensions thereof) was almost exclusively due to Hausdorff.[13]

The "Magnum Opus": "Principles of set theory"

According to former notions, set theory included not only the general set theory and the theory of sets of points, but also dimension and measure theory. Hausdorff's work was the first textbook which presented all of set theory in this broad sense, systematically and with full proofs. Hausdorff was aware of how easily the human mind can err while also seeking for rigor and truth. So he proposed in the preface of the work:

"... Of the human privilege of error to make as economical a use as possible."

This book went far beyond its masterful portrayal of the known. It also contained a series of important original contributions of the author that can only be hinted at in the following.

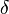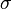The first six chapters deal with the basic concepts of the general set theory. At the beginning Hausdorff sets forth a detailed set algebra with some pioneering new concepts (differences chains, set rings and set fields, \delta- and \sigma-systems). These introductory paragraphs on sets and their connections included, for example, the modern set-theoretic notion of functions. Next followed in Chapters 3 to 5 the classical theory of cardinal numbers, order types and ordinals. In the sixth chapter "Relations between ordered and well-ordered sets" Hausdorff presents, among other things, the most important results of his own research on ordered sets.

In the chapters on "point sets" - the topological chapters - Hausdorff developed for the first time, based on the known neighborhood axioms, a systematic theory of topological spaces, where in addition he added the separation axiom later named after him. This theory emerges from a comprehensive synthesis of earlier approaches of other mathematicians and Hausdorff's own reflections on the problem of space. The concepts and theorems of classical point set theory 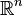\mathbb{R}^n are - as far as possible - transferred to the general case, and thus become part of the newly created general or set-theoretic topology. But Hausdorff not only performed this "translation work", but he developed also basic construction method of topology as nucleation (interior, dense-in-itself core) and shell formation (closure), and he works the fundamental importance of the concept of open set (called "area" by him) and of the compactness introduced by Fréchet. He also founded and developed the theory of the connected set, particularly through the introduction of the terms "component" and "quasi-component".

By the first and eventually the second Hausdorff countability axioms the considered spaces were gradually further specialized. A large class of spaces satisfying the countable first axiom are metric spaces. They were introduced in 1906 by Fréchet under the name "classes (E)". The term "metric space" comes from Hausdorff. In Principles, he developed the theory of metric spaces and systematically enriched it through a series of new concepts: Hausdorff metric, complete, total boundedness, \rho-connectivity, reducible sets. Fréchets work had been little noticed; only through Hausdorff's Principles did metric spaces become the common property of the mathematician.

The chapter on illustrations and the final chapter of Principles on measure and integration theory are enriched by the generality of the material and the originality of presentation. Hausdorff's mention of the importance of measure theory for probability had great historical effect, despite its laconic brevity. One finds in this chapter the first correct proof of the strong law of large numbers of Émile Borel. Finally, the appendix contains the single most spectacular result of the whole book, namely Hausdorff's theorem that one cannot define a volume for all bounded subsets of 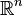\mathbb{R}^n for n \geq 3. The proof is based on Hausdorff's paradoxical ball decomposition, whose production requires the axiom of choice.[14]

During the 20th Century, it became the standard to build mathematical theories on axiomatic set theory. The creation of axiomatically founded generalized theories, such as the general topology, served among other things to single out the common structural core for various specific cases or regions and then set up an abstract theory, which contained all these parts as special cases. This brought a great success in the form of simplification and harmonization and ultimately brought on economy of thought with itself. Hausdorff himself highlighted this aspect in the Principles. The topological chapter the basic concepts are methodologically a pioneering effort, and they showed the way for the development of modern mathematics.

Principles of set theory appeared in an already tense time on the eve of the First World War. In August 1914, the war, which also dramatically affected the scientific life in Europe. Under these circumstances, could hardly be effective Hausdorff's book in the first five to six years after its appearance. After the war, a new generation of young researchers set forth to expand on the suggestions that were included in this work in such abundance, and with no doubt, the topology was the focus of attention. The journal Fundamenta Mathematicae played a special role in the reception of Hausdorff ideas, founded in Poland in 1920. It was one of the first mathematical journals with special emphasis on set theory, topology, theory of real functions, measure and integration theory, functional analysis, logic and foundations of mathematics. In this spectrum, a special focus was the general topology. Hausdorff's Principles were present in Fundamenta Mathematicae from the first volume in a remarkable frequency. Of the 558 works (Hausdorff's own three works not calculated), which appeared in the first twenty volumes from 1920 to 1933, 88 cite Principles. One even has to take into account that as Hausdorff's conceptions increasingly became commonplace, so they were also used in a number of works that did not mention it explicitly. The Russian topological school, founded by Paul Alexandroff and Urysohn Paul, was based heavily on Hausdorff's Principles. This is shown by the surviving correspondence in Hausdorff's Nachlass with Urysohn, and especially Alexandroff and Urysohn's Mémoire sur les multiplicités Cantoriennes,[15] a work the size of a book, in which Urysohn developed dimension theory and Principles is cited no less than 60 times.

Long after the Second World War there was a strong demand for Hausdorff's book, and there were three reprints at Chelsea from 1949, 1965 and 1978.

Descriptive set theory, measure theory and analysis

In 1916, Alexandroff and Hausdorff independently solved[16] the continuum problem for Borel sets : Every Borel set in a complete separable metric space is either countable or has the cardinality of the continuum. This result generalizes the Cantor-Bendixson theorem that such a statement holds for the closed sets of 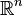\mathbb{R}^n. For linear G_{\delta} sets William Henry Young had proved the result in 1903,[17] for G_{\delta\sigma\delta} sets Hausdorff obtained a corresponding result in 1914 in the Principles. The theorem of Alexandroff and Hausdorff was a strong impetus for further development of descriptive set theory.[18]

Among the publications of Hausdorff in his time at Greifswald time the work Dimension and outer measure from 1919 is particularly outstanding. It has remained highly topical and in later years has been probably the most cited mathematical original work from the decade from 1910 to 1920. In this work, the concepts were introduced which are now known as Hausdorff measure and the Hausdorff dimension.

Hausdorff dimension term is a fine instrument for the characterization and comparison of "highly rugged quantities". The concepts of Dimension and outer measure have experienced applications and further developments in many areas such as in the theory of dynamical systems, geometric measure theory, the theory of self-similar sets and fractals, the theory of stochastic processes, harmonic analysis, potential theory and number theory.[19]

Significant analytical work of Hausdorff occurred in his second time at Bonn. In Summation methods and moment sequences I in 1921, he developed a whole class of summation methods for divergent series, which today are called Hausdorff methods. In Hardy's classic Divergent Series, an entire chapter is devoted to the Hausdorff method. The classical methods of Hölder and Cesàro proved to be special Hausdorff method. Every Hausdorff method is given by a moment sequence; in this context Hausdorff gave an elegant solution of the moment problem for a finite interval, bypassing the theory of continued fractions. In Moment problems for a finite interval of 1923 he treated more special moment problems, such as those with certain restrictions for generating density 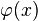\varphi(x), for instance \varphi(x) \in L^p[0,1]. Criteria for solvability and determination of moment problems occupied Hausdorff for many years as hundreds of pages of studies in his Nachlass attest.[20]

A significant contribution to the emerging functional analysis in the twenties was Hausdorff's extension of the Riesz-Fischer theorem toL^p spaces in his 1923 work An extension of Parseval's theorem on Fourier series. He proved the inequalities now named after him and W.H. Young. The Hausdorff-Young inequalities became the starting point of major new developments.[21]

Hausdorff's bookSet Theory appeared in 1927. This was declared as a second Edition of Principles, but it was actually a completely new book. Since the scale was significantly reduced due to its appearance in Goschen's teaching library, large parts of the theory of ordered sets and measures and integration theory were removed. "More than these deletions, the reader will perhaps regret" (said Hausdorff in the preface), "that I, to further save space in point set theory, have abandoned the topological point of view through which the first edition has apparently acquired many friends have limited myself to the easier theory of metric spaces".

In fact, this was an explicit regret of some reviewers of the work. As a kind of compensation Hausdorff showed for the first time the then current state of descriptive set theory. This fact assured the book almost as intense a reception as Principles, especially in Fundamenta Mathematicae. As a textbook it was very popular. In 1935 there was an expanded edition published, and this was reprinted by Dover in 1944. An English translation appeared in 1957 with reprints in 1962 and 1967.

There was also a Russian edition (1937), which although it was only partially a faithful translation, and partly a reworking by Alexandroff and Kolmogorov. In this translation the topological point of view again moved to the forefront. In 1928 a review of Set Theory appeared from the pen of Hans Hahn. Perhaps Hahn had the danger of German anti-Semitism in his mind as he closed this discussion with the following sentence:

"An exemplary depiction in every respect of a difficult and thorny area, a work on par with those which have carried the fame of German science about the world and such that all German mathematicians may be proud with."ref=[22]}

The last works

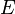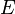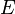In his last work Erweiterung einer stetigen Abbildung Hausdorff showed in 1938 that a continuous function from a closed subset F of a metric space E can be extended to all of E (although the image may need to be extended). As a special case, every homeomorphism from F can be extended to a homeomorphism from E. This work set forth results from earlier years. In 1919, in Über halbstetige Funktionen und deren Verallgemeinerung, Hausdorff had, among other things, given another proof of the Tietze extension theorem. In 1930 in Erweiterung einer Homöomorphie (extending a homeomorphism) he showed the following: Let 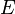E be a metric space, 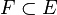F \subset E a closed subset. If F is given a new metric without changing the topology, this metric can be extended to the entire space without changing the topology. The work Gestufte Räume appeared in 1935. Here Hausdorff discussed spaces which fulfilled the Kuratowski closure axioms up to just the axiom of idempotence. He named them ``graded spaces (often also called closure spaces) used them in the study of the relationships between the Fréchet limit spaces and topological spaces.

Hausdorff as name giver

The Name Hausdorff is found throughout mathematics. Among others, these concepts were named after him:

In the universities of Bonn and Greifswald, these things were named in his honor:

Besides these, in Bonn there is the Hausdorffstraße (Hausdorff Street), where he first lived. (Haus-Nr. 61). In Greifswald there is a Felix-Hausdorff-Straße, where the Institutes for Biochemistry and Physics are located, among others. Since 2011, there is a "Hausdorffweg" (Hausdorff-Way) in the middle of Leipziger Ortsteil Gohlis.[23]

The Asteroid (24947) Hausdorff was named after him.

Writings

As Paul Mongré

Only a selection of the essays that appeared in text are shown here.

As Felix Hausdorff

Collected works

The "Hausdorff-Edition“, edited by E. Brieskorn, F. Hirzebruch, W. Purkert (all Bonn), R. Remmert (Münster) und E. Scholz (Wuppertal) with the collaboration of over twenty mathematicians, historians, philosophers and scholars, will present the works of Hausdorff, with commentary and much additional material. The edition is an ongoing project of the Nordrhein-Westfälischen Akademie der Wissenschaften und der Künste. The planned nine volumes are being published by Springer-Verlag, Heidelberg. As of 2008, five had appeared. See the Home page of the Hausdorff Project Homepage of the Hausdorff Edition (German) for its current status and further information. The projected volumes are:

References

See also

References

  1. ↑ Archiv der Universität Leipzig, PA 547
  2. ↑ Gabbay, Dov M. (2012-01-01). Handbook of the History of Logic: Sets and extensions in the twentieth century. Elsevier. ISBN 9780444516213.
  3. ↑ Neuenschwander, E.: Felix Hausdorffs letzte Lebensjahre nach Dokumenten aus dem Bessel-Hagen-Nachlaß. In: Brieskorn 1996, S. 253–270.
  4. ↑ Nachlass Bessel-Hagen, Universitätsarchiv Bonn. Abgedruckt in Brieskorn 1996, S. 263–264 und im Faksimile S. 265–267
  5. ↑
    Wikisource has original text related to this article:
  6. ↑ Siehe Findbuch Nachlass Hausdorff
  7. ↑ Niedersächsische Staats- und Universitätsbibliothek zu Göttingen, Handschriftenabteilung, NL Hilbert, Nr. 136.
  8. ↑ Detaillierte Angaben findet man in den gesammelten Werken, Band II, S. 9-12.
  9. ↑ H.: Gesammelte Werke. Band II: Grundzüge der Mengenlehre. Springer-Verlag, Berlin, Heidelberg etc. 2002. Kommentare von U. Felgner, S. 598-601.
  10. ↑ H.: Gesammelte Werke. Band II: Grundzüge der Mengenlehre. Springer-Verlag, Berlin, Heidelberg etc. 2002. S. 604-605.
  11. ↑ Siehe dazu den Essay von U. Felgner: Die Hausdorffsche Theorie der 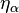\eta_{\alpha}-Mengen und ihre Wirkungsgeschichte in H.: Gesammelte Werke. Band II: Grundzüge der Mengenlehre. Springer-Verlag, Berlin, Heidelberg etc. 2002. S. 645-674.
  12. ↑ Siehe dazu und zu ähnlichen Sätzen von Kuratowski und Zorn den Kommentar von U. Felgner in den gesammelten Werken, Band II, S. 602-604.
  13. ↑ Schoenflies, A.: Die Entwickelung der Lehre von den Punktmannigfaltigkeiten. Teil II. Jahresbericht der DMV, 2. Ergänzungsband, Teubner, Leipzig 1908., S. 40.
  14. ↑ Zur Wirkungsgeschichte des Hausdorffschen Kugelparadoxons siehe Gesammelte Werke Band IV, S. 11-18; ferner den Aufsatz von P. Schreiber in Brieskorn 1996, S. 135-148, und die Monographie Wagon 1993.
  15. ↑ Urysohn, P.: Mémoire sur les multiplicités Cantoriennes. (PDF; 6,2 MB) Fundamenta Mathematicae 7 (1925), S. 30-137; 8 (1926), S. 225-351.
  16. ↑ P. Alexandroff: Sur la puissance des ensembles mesurables B. Comptes rendus Acad. Sci. Paris 162 (1916), S. 323–325.
  17. ↑ W. H. Young: Zur Lehre der nicht abgeschlossenen Punktmengen. Berichte über die Verhandlungen der Königl. Sächs. Ges. der Wiss. zu Leipzig, Math.-Phys. Klasse 55 (1903), S. 287-293.
  18. ↑ Alexandorff, Hopf 1935, S. 20. Für nähere Angaben siehe Gesammelte Werke Band II, S. 773–787.
  19. ↑ Zur Wirkungsgeschichte von Dimension und äußeres Maß siehe die Artikel von Bandt/Haase und Bothe/Schmeling in Brieskorn 1996, S. 149–183 und S. 229–252 sowie den Kommentar von S. D. Chatterji in den Gesammelten Werken, Band IV, S. 44–54 und die dort angegebene Literatur.
  20. ↑ Zum Gesamtkomplex dieser Arbeiten und Nachlassstudien siehe Gesammelte Werke Band IV, S. 105–171, 191–235, 255–267 und 339–373.
  21. ↑ Siehe dazu den Kommentar von S. D. Chatterji in den Gesammelten Werken Band IV, S. 182–190.
  22. ↑ Hahn, H. (1928). "F. Hausdorff, Mengenlehre". Monatshefte für Mathematik und Physik 35: 56–58.
  23. ↑ Ratsversammlung vom 18. Mai 2011 (Beschluss-Nr. RBV-822/11), amtliche Bekanntmachung: Leipziger Amtsblatt Nr. 11 vom 4. Juni 2011, bestandskräftig seit dem 5. Juli 2011 bzw. 5. August 2011. Vgl. Leipziger Amtsblatt Nr. 16 vom 10. September 2011.
  24. 1 2 3 4 Gray, Jeremy (2007). "Review: Gesammelte Werke, Vols. II, IV, V, and VII, by Felix Hausdorff" (PDF). Bull. Amer. Math. Soc. (N.S.) 44 (3): 471–474. doi:10.1090/S0273-0979-07-01137-8.

External links

This article is issued from Wikipedia - version of the Saturday, February 06, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.