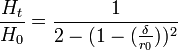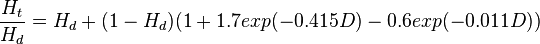Fåhræus effect
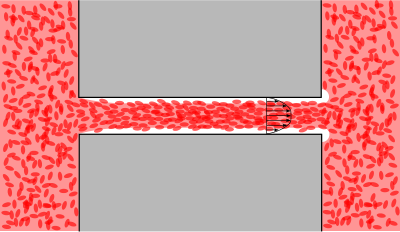
The Fåhræus effect is the decrease in average concentration of red blood cells in human blood as the diameter of the glass tube in which it is flowing decreases. In other words, in blood vessels with diameters less than 500 micrometers, both the hematocrit decreases with decreasing capillary diameter. The Fåhræus effect definitely influences the Fåhræus–Lindqvist effect, which describes the dependence of apparent viscosity of blood on the capillary size, but the former is not the only cause of the latter.[1]
Mathematical model
Considering steady laminar fully developed blood flow in a small tube with radius of  , whole blood separates into a cell-free plasma layer along the tube wall and enriched central core. As a result, the tube hematocrit
, whole blood separates into a cell-free plasma layer along the tube wall and enriched central core. As a result, the tube hematocrit 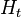 is smaller than the out flow hematocrit
is smaller than the out flow hematocrit 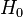 .
A simple mathematical treatment of the Fåhræus effect was shown in Sutera et al. (1970).[2] This seems to be the earliest analysis:
.
A simple mathematical treatment of the Fåhræus effect was shown in Sutera et al. (1970).[2] This seems to be the earliest analysis:
where:
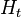 is the tube hematocrit
is the tube hematocrit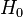 is the outlet hematocrit
is the outlet hematocrit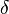 is the cell-free plasma layer thickness
is the cell-free plasma layer thickness is the radius of the tube
is the radius of the tube
Also, the following expression was developed by Pries et al. (1990)[3] to represent tube hematocrit,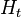 , as a function of discharge hematocrit,
, as a function of discharge hematocrit,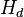 , and tube diameter.
, and tube diameter.
where:
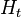 is the tube hematocrit
is the tube hematocrit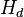 is the discharge hematocrit
is the discharge hematocrit is the diameter of the tube in µm
is the diameter of the tube in µm
Further reading
- C. Kleinstrauer, (2007) Bio-Fluid Dynamics, Taylor and Francis Pub.
See also
References
- ↑ "Blood Flow and Fahraeus Effect". Nonoscience.info. 2010-09-02. Retrieved 2011-05-09.
- ↑ "Capillary blood flow: II. Deformable model cells in tube flow". Microvascular Research 2 (4): 420–433. 1970. doi:10.1016/0026-2862(70)90035-X.
- ↑ Pries AR, Secomb TW, Gaehtgens P and Gross JF. Blood flow in microvascular networks: Experiments and simulation. Circulation Research 67:826-834, 1990.