Extreme value theory

This article is about the extreme value theory in statistics. For the result in calculus, see extreme value theorem.

Extreme value theory is used to model the risk of extreme, rare events, such as the 1755 Lisbon earthquake.

Extreme value theory or extreme value analysis (EVA) is a branch of statistics dealing with the extreme deviations from the median of probability distributions. It seeks to assess, from a given ordered sample of a given random variable, the probability of events that are more extreme than any previously observed. Extreme value analysis is widely used in many disciplines, such as structural engineering, finance, earth sciences, traffic prediction, and geological engineering. For example, EVA might be used in the field of hydrology to estimate the probability of an unusually large flooding event, such as the 100-year flood. Similarly, for the design of a breakwater, a coastal engineer would seek to estimate the 50-year wave and design the structure accordingly.

Data analysis

Two approaches exist for practical extreme value analysis. The first method relies on deriving block maxima (minima) series as a preliminary step. In many situations it is customary and convenient to extract the annual maxima (minima), generating an "Annual Maxima Series" (AMS). The second method relies on extracting, from a continuous record, the peak values reached for any period during which values exceed a certain threshold (falls below a certain threshold). This method is generally referred to as the "Peak Over Threshold" ^[1] method (POT) and can lead to several or no values being extracted in any given year.

For AMS data, the analysis may partly rely on the results of the Fisher–Tippett–Gnedenko theorem, leading to the generalized extreme value distribution being selected for fitting.^[2]^[3] However, in practice, various procedures are applied to select between a wider range of distributions. The theorem here relates to the limiting distributions for the minimum or the maximum of a very large collection of independent random variables from the same arbitrary distribution. Given that the number of relevant random events within a year may be rather limited, it is unsurprising that analyses of observed AMS data often lead to distributions other than the generalized extreme value distribution being selected.^[4]

For POT data, the analysis involves fitting two distributions: one for the number of events in a basic time period and a second for the size of the exceedances. A common assumption for the first is the Poisson distribution, with the generalized Pareto distribution being used for the exceedances. Some further theory needs to be applied in order to derive the distribution of the most extreme value that may be observed in a given period, which may be a target of the analysis. An alternative target may be to estimate the expected costs associated with events occurring in a given period. For POT analyses, a tail-fitting can be based on the Pickands–Balkema–de Haan theorem.^[5]^[6]

Applications

Applications of extreme value theory include predicting the probability distribution of:

Extreme floods
The amounts of large insurance losses
Equity risks
Day to day market risk
The size of freak waves
Mutational events during evolution
Large wildfires^[7]
Environmental loads on structures^[8]
It can be applied to some characterization of the distribution of the maxima of incomes, like in some surveys done in virtually all the National Offices of Statistics
Estimate fastest time humans are capable of running the 100 metres sprint^[9] and performances in other athletic disciplines.,^[10]^[11]
Pipeline failures due to pitting corrosion.

History

The field of extreme value theory was pioneered by Leonard Tippett (1902–1985). Tippett was employed by the British Cotton Industry Research Association, where he worked to make cotton thread stronger. In his studies, he realized that the strength of a thread was controlled by the strength of its weakest fibres. With the help of R. A. Fisher, Tippet obtained three asymptotic limits describing the distributions of extremes. Emil Julius Gumbel codified this theory in his 1958 book Statistics of Extremes, including the Gumbel distributions that bear his name.

A summary of historically important publications relating to extreme value theory can be found on the article List of publications in statistics.

Univariate theory

Let $X_1, \dots, X_n$ be a sequence of independent and identically distributed variables with distribution function F and let $M_n =\max(X_1,\dots,X_n)$ denote the maximum.

In theory, the exact distribution of the maximum can be derived:

\begin{align} \Pr(M_n \leq z) & = \Pr(X_1 \leq z, \dots, X_n \leq z) \\ & = \Pr(X_1 \leq z) \cdots \Pr(X_n \leq z) = (F(z))^n. \end{align}

The associated indicator function $I_n = I(M_n>z)$ is a Bernoulli process with a success probability 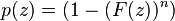$p(z)=(1-(F(z))^n)$ that depends on the magnitude 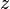$z$ of the extreme event. The number of extreme events within $n$ trials thus follows a binomial distribution and the number of trials until an event occurs follows a geometric distribution with expected value and standard deviation of the same order $O(1/p(z))$ .

In practice, we might not have the distribution function $F$ but the Fisher–Tippett–Gnedenko theorem provides an asymptotic result. If there exist sequences of constants $a_n>0$ and $b_n\in \mathbb R$ such that

\Pr\{(M_n-b_n)/a_n \leq z\} \rightarrow G(z)

as $n \rightarrow \infty$ then

G(z) \propto \exp \left[-(1+\zeta z)^{-1/\zeta} \right]

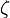where $\zeta$ depends on the tail shape of the distribution. When normalized, G belongs to one of the following non-degenerate distribution families:

Weibull law: $G(z) = \begin{cases} \exp\left\{-\left( -\left( \frac{z-b}{a} \right) \right)^\alpha\right\} & z<b \\ 1 & z\geq b \end{cases}$ when the distribution of $M_n$ has a light tail with finite upper bound. Also known as Type 3.

Gumbel law: $G(z) = \exp\left\{-\exp\left(-\left(\frac{z-b}{a}\right)\right)\right\}\text{ for }z\in\mathbb R.$ when the distribution of $M_n$ has an exponential tail. Also known as Type 1

Fréchet Law: $G(z) = \begin{cases} 0 & z\leq b \\ \exp\left\{-\left(\frac{z-b}{a}\right)^{-\alpha}\right\} & z>b. \end{cases}$ when the distribution of $M_n$ has a heavy tail (including polynomial decay). Also known as Type 2.

In all cases, $\alpha>0$ .

Notes

↑ Leadbetter (1991)
↑ Fisher and Tippett (1928)
↑ Gnedenko (1943)
↑ Embrechts, Klüppelberg, and Mikosch (1997)
↑ Pickands (1975)
↑ Balkema and de Haan (1974)
↑ Alvardo (1998, p.68.)
↑ Makkonen (2008)
↑ J.H.J. Einmahl & S.G.W.R. Smeets (2009), "Ultimate 100m World Records Through Extreme-Value Theory", CentER Discussion Paper, Tilburg University 57, retrieved 2009-08-12
↑ D. Gembris, J.Taylor & D. Suter (2002), "Trends and random fluctuations in athletics", Nature 417: 506, doi:10.1038/417506a
↑ D. Gembris, J.Taylor & D. Suter (2007), "Evolution of athletic records : Statistical effects versus real improvements", Journal of Applied Statistics 34 (5): 529–545, doi:10.1080/02664760701234850, retrieved 2014-01-03

References

Abarbane, H.; Koonin, S.; Levine, H.; MacDonald, G.; Rothaus, O. (January 1992), "Statistics of Extreme Events with Application to Climate" (PDF), JASON, JSR-90-30S, retrieved 2015-03-03
Alvarado, Ernesto; Sandberg, David V.; Pickford, Stewart G. (1998), "Modeling Large Forest Fires as Extreme Events" (PDF), Northwest Science 72: 66–75, retrieved 2009-02-06
Balkema, A.; Laurens (1974), "Residual life time at great age", Annals of Probability 2: 792–804, doi:10.1214/aop/1176996548, JSTOR 2959306
Burry K.V. (1975). Statistical Methods in Applied Science. John Wiley & Sons.
Castillo E. (1988) Extreme value theory in engineering. Academic Press, Inc. New York. ISBN 0-12-163475-2.
Castillo,E., Hadi,A. S., Balakrishnan, N. and Sarabia, J. M. (2005) Extreme Value and Related Models with Applications in Engineering and Science, Wiley Series in Probability and Statistics Wiley, Hoboken, New Jersey. ISBN 0-471-67172-X.
Coles S. (2001) An Introduction to Statistical Modeling of Extreme Values. Springer, London.
Embrechts P., Klüppelberg C. and Mikosch T. (1997) Modelling extremal events for insurance and finance. Berlin: Spring Verlag
Fisher, R.A.; Tippett, L.H.C. (1928), "Limiting forms of the frequency distribution of the largest and smallest member of a sample", Proc. Cambridge Phil. Soc. 24: 180–190, doi:10.1017/s0305004100015681
Gnedenko, B.V. (1943), "Sur la distribution limite du terme maximum d'une serie aleatoire", Annals of Mathematics 44: 423–453, doi:10.2307/1968974
Gumbel, E.J. (1935), "Les valeurs extrêmes des distributions statistiques" (PDF), Ann. Inst. Henri Poincaré 5 (2): 115–158, retrieved 2009-04-01
Gumbel, Emil J. (2004) [1958], Statistics of Extremes, Mineola, NY: Dover, ISBN 0-486-43604-7
Makkonen, L. (2008), "Problems in the extreme value analysis", Structural Safety 30: 405–419, doi:10.1016/j.strusafe.2006.12.001
Leadbetter, M. R. (1991), "On a basis for 'Peaks over Threshold' modeling", Statistics & Probability Letters 12 (4): 357–362, doi:10.1016/0167-7152(91)90107-3
Leadbetter M.R., Lindgren G. and Rootzen H. (1982) Extremes and related properties of random sequences and processes. Springer-Verlag, New York.
Lindgren, G.; Rootzen, H. (1987), "Extreme values: Theory and technical applications", Scandinavian Journal of Statistics, Theory and Applications 14: 241–279
Novak S.Y. (2011) Extreme Value Methods with Applications to Finance. Chapman & Hall/CRC Press, London. ISBN 978-1-4398-3574-6
Pickands, J (1975), "Statistical inference using extreme order statistics", Annals of Statistics 3: 119–131

External links

This article is issued from Wikipedia - version of the Tuesday, February 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.