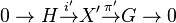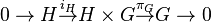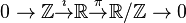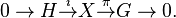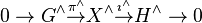Extension of a topological group
In mathematics, more specifically in topological groups, an extension of topological groups, or a topological extension, is a short exact sequence 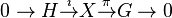 where
where 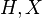 and
and  are topological groups and
are topological groups and  and
and 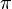 are continuous homomorphisms which are also open onto their images.[1] Every extension of topological group is therefore a group extension
are continuous homomorphisms which are also open onto their images.[1] Every extension of topological group is therefore a group extension
Classification of extensions of topological groups
We say that the topological extensions
and
are equivalent (or congruent) if there exists a topological isomorphism 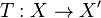 making commutative the diagram of Figure 1.
making commutative the diagram of Figure 1.

We say that the topological extension
is a split extension (or splits) if it is equivalent to the trivial extension
where 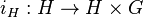 is the natural inclusion over the first factor and
is the natural inclusion over the first factor and 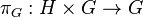 is the natural projection over the second factor.
is the natural projection over the second factor.
It is easy to prove that the topological extension 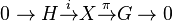 splits if and only if there is a continuous homomorphism
splits if and only if there is a continuous homomorphism 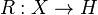 such that
such that 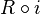 is the identity map on
is the identity map on 
Note that the topological extension 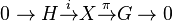 splits if and only if the subgroup
splits if and only if the subgroup 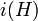 is a topological direct summand of
is a topological direct summand of 
Examples
- Take
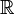 the real numbers and
the real numbers and  the integer numbers. Take
the integer numbers. Take  the natural inclusion and
the natural inclusion and 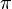 the natural projection. Then
the natural projection. Then
- is an extension of topological abelian groups. Indeed it is an example of a non-splitting extension.
Extensions of locally compact abelian groups (LCA)
An extension of topological abelian groups will be a short exact sequence 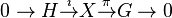 where
where 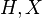 and
and  are locally compact abelian groups and
are locally compact abelian groups and  and
and 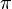 are relatively open continuous homomorphisms.[2]
are relatively open continuous homomorphisms.[2]
- Let be an extension of locally compact abelian groups
-
- Take
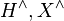 and
and 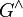 the Pontryagin duals of
the Pontryagin duals of 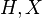 and
and  and take
and take 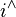 and
and 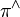 the dual maps of
the dual maps of  and
and 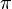 . Then the sequence
. Then the sequence
-
- is an extension of locally compact abelian groups.
References
- ↑ Cabello Sánchez, Félix (2003). "Quasi-homomorphisms". Fundam. Math. 178 (3): 255–270. doi:10.4064/fm178-3-5. Zbl 1051.39032.
- ↑ Fulp, R.O.; Griffith, P.A. (1971). "Extensions of locally compact abelian groups. I, II" (PDF). Trans. Am. Math. Soc. 154: 341–356, 357–363. doi:10.1090/S0002-9947-1971-99931-0. MR 0272870. Zbl 0216.34302.