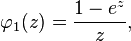Exponential integrator
Exponential integrators are a class of numerical methods for the solution of partial and ordinary differential equations. This large class of methods from numerical analysis is based on the exact integration of the linear part of the initial value problem described later in this article. Because the linear part is integrated exactly, this can help to mitigate the stiffness of a differential equation. Exponential integrators can be constructed to be explicit or implicit for numerical ordinary differential equations or serve as the time integrator for numerical partial differential equations.
Background
Dating back to at least the 1960s, these methods were recognized by Certain[1] and Pope.[2] As of late exponential integrators have become an active area of research. Originally developed for solving stiff differential equations, the methods have been used to solve partial differential equations including hyperbolic as well as parabolic problems[3] such as the heat equation.
Introduction
We consider initial value problems of the form,
where  is composed of linear terms,
and
is composed of linear terms,
and 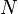 is composed of the non-linear terms.
These problems can come from a more typical initial value problem
is composed of the non-linear terms.
These problems can come from a more typical initial value problem
after linearizing locally about a fixed or local state 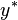 :
:
Here, 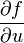 refers to the partial derivative of
refers to the partial derivative of  with respect to
with respect to 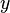 .
.
Exact integration of this problem from time 0 to a later time  can be performed using matrix exponentials to define an integral equation for the exact solution:[4]
can be performed using matrix exponentials to define an integral equation for the exact solution:[4]
This is similar to the exact integral used in the Picard–Lindelöf theorem. In the case of 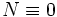 , this formulation is the exact solution to the linear differential equation.
, this formulation is the exact solution to the linear differential equation.
Numerical methods require a discretization of equation (2). They can be based on Runge-Kutta discretizations,[5][6] linear multistep methods or a variety of other options.
Exponential Rosenbrock methods
In order to improve the stability when integrating the nonlinearity 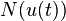 , one can use a continuous linearization of (1) along the numerical solution
, one can use a continuous linearization of (1) along the numerical solution  to get
to get
where
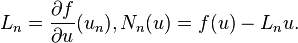 This offers a great advantage which is
This offers a great advantage which is
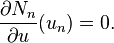 Again, applying the variation-of-constants formula (2) gives the exact solution at time
Again, applying the variation-of-constants formula (2) gives the exact solution at time 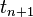 as
as
The idea is to approximate the integral in (4) by some quadrature rule with nodes 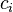 and weights
and weights 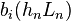 (
(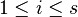 ).
This yields exponential Rosenbrock methods, see :[4]
).
This yields exponential Rosenbrock methods, see :[4]
By introducing the difference 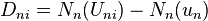 , they can be reformulated in a more efficient way (for implementation) as
, they can be reformulated in a more efficient way (for implementation) as
Examples
See also: the first-order exponential integrator for more details.
First-order forward Euler exponential integrator
The simplest method is based on a forward Euler time discretization. It can be realized
by holding the term 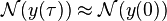 constant over the whole interval.
Exact integration of
constant over the whole interval.
Exact integration of 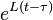 then results in the
then results in the
Of course, this process can be repeated over small intervals to serve as the basis of a single-step numerical method.
In general, one defines a sequence of functions,
that show up in these methods. Usually, these linear operators are not computed exactly, but a Krylov subspace iterative method can be used to efficiently compute the multiplication of these operators times vectors.[7] See references for further details of where these functions come from.[5][8]
Fourth-order ETDRK4 method of Cox and Mathews
Cox and Mathews[9] describe a fourth-order method exponential time differencing (ETD) method that they used Maple to derive.
We use their notation, and assume that the unknown function is 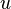 , and that we have a known solution
, and that we have a known solution  at time
at time  .
Furthermore, we'll make explicit use of a possibly time dependent right hand side:
.
Furthermore, we'll make explicit use of a possibly time dependent right hand side: 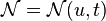 .
.
Three stage values are first constructed:
The final update is given by,
If implemented naively, the above algorithm suffers from numerical instabilities due to floating point round-off errors.[10] To see why, consider the first function,
which is present in the first-order Euler method, as well as all three stages of ETDRK4. For small values of 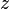 , this function suffers from numerical cancellation errors. However, these numerical issues can be avoided by evaluating the
, this function suffers from numerical cancellation errors. However, these numerical issues can be avoided by evaluating the  function via a contour integral approach [10] or by a Padé approximant.[11]
function via a contour integral approach [10] or by a Padé approximant.[11]
Applications
Exponential integrator are used for the simulation of stiff scenarios in scientific and visual computing, for example in molecular dynamics,[12] for VLSI circuit simulation,[13] and in computer graphics.[14] They are also applied in the context of hybrid monte carlo methods.[15] In these applications, exponential integrators show the advantage of large time stepping capability and high accuracy. To accelerate the evaluation of matrix functions in such complex scenarios, exponential integrators are often combined with Krylov subspace projection methods.
See also
- General linear methods
- Linear multistep methods
- Numerical analysis
- Numerical methods for ordinary differential equations
- Runge-Kutta methods
Notes
- ↑ Certain (1960)
- ↑ Pope (1963)
- ↑ Hochbruck and Ostermann, (2006)
- 1 2 Hochbruck and Ostermann, (2010)
- 1 2 Cox and Mathews (2002)
- ↑ Tokman (2006, 2011)
- ↑ Tokman (2006, 2010)
- ↑ Hochbruck and Ostermann (2010)
- ↑ Cox and Mathews 2002
- 1 2 Kassam and Trefethen (2005)
- ↑ Berland et al. (2007)
- ↑ Michels and Desbrun (2015)
- ↑ Zhuang et al. (2014)
- ↑ Michels et al. (2014)
- ↑ Chao et al. (2015)
References
- Berland, Havard; Owren, Brynjulf; Skaflestad, Bard (2005). "B-series and Order Conditions for Exponential Integrators". SIAM Journal of Numerical Analysis 43 (4): 1715–1727. doi:10.1137/040612683.
- Berland, Havard; Skaflestad, Bard; Wright, Will M. (2007). "EXPINT-A MATLAB Package for Exponential Integrators". ACM Transactions on Mathematical Software 33 (1). doi:10.1145/1206040.1206044.
- Chao, Wei-Lun; Solomon, Justin; Michels, Dominik L.; Sha, Fei (2015). "Exponential Integration for Hamiltonian Monte Carlo". Proceedings of the 32nd International Conference on Machine Learning (ICML-15): 1142–1151.
- Certaine, John (1960). The solution of ordinary differential equations with large time constants. Wiley. pp. 128–132.
- Cox, S. M.; Mathews, P.C. (March 2002). "Exponential time differencing for stiff systems". Journal of Computational Physics 176 (2): 430–455. doi:10.1006/jcph.2002.6995.
- Hochbruck, Marlis; Ostermann, Alexander (May 2010). "Exponential integrators". Acta Numer. 19: 209–286. doi:10.1017/S0962492910000048.
- Hochbruck, Marlis; Ostermann, Alexander (2005). "Explicit exponential Runge-Kutta methods for semilinear parabolic problems". SIAM Journal of Numerical Analysis 43 (3): 1069–1090. doi:10.1137/040611434.
- Hochbruck, Marlis; Ostermann, Alexander (May 2005). "Exponential Runge–Kutta methods for parabolic problems". Applied Numerical Mathematics 53 (2-4): 323–339. doi:10.1016/j.apnum.2004.08.005.
- Luan, Vu Thai; Ostermann, Alexander (2014). "Exponential Rosenbrock methods of order five-construction, analysis and numerical comparisons". Journal of Computational and Applied Mathematics 255: 417–431. doi:10.1016/j.cam.2013.04.041.
- Luan, Vu Thai; Ostermann, Alexander (2014). "Explicit exponential Runge-Kutta methods of high order for parabolic problems". Journal of Computational and Applied Mathematics 256: 168–179. doi:10.1016/j.cam.2013.07.027.
- Luan, Vu Thai; Ostermann, Alexander (2013). "Exponential B-series: The stiff case". SIAM Journal of Numerical Analysis 51: 3431–3445. doi:10.1137/130920204.
- Luan, Vu Thai; Ostermann, Alexander (2014). Stiff order conditions for exponential Runge-Kutta methods of order five. Modeling, Simulation and Optimization of Complex Processes - HPSC 2012 (H.G. Bock et al. eds.). pp. 133–143. doi:10.1007/978-3-319-09063-4_11.
- Michels, Dominik L.; Desbrun, Mathieu (2015). "A Semi-analytical Approach to Molecular Dynamics". Journal of Computational Physics 303: 336–354. doi:10.1016/j.jcp.2015.10.009.
- Michels, Dominik L.; Sobottka, Gerrit A.; Weber, Andreas G. (2014). "Exponential Integrators for Stiff Elastodynamic Problems". ACM Transactions on Graphics 33: 7:1–7:20. doi:10.1145/2508462.
- Pope, David A (1963). "An exponential method of numerical integration of ordinary differential equations". Communications of the ACM 6 (8): 491–493. doi:10.1145/366707.367592.
- Tokman, Mayya (October 2011). "A new class of exponential propagation iterative methods of Runge–Kutta type (EPIRK)". Journal of Computational Physics 230 (24): 8762–8778. doi:10.1016/j.jcp.2011.08.023.
- Tokman, Mayya (April 2006). "Efficient integration of large stiff systems of ODEs with exponential propagation iterative (EPI) methods". Journal of Computational Physics 213 (2): 748–776. doi:10.1016/j.jcp.2005.08.032.
- Trefethen, Lloyd N.; Aly-Khan Kassam (2005). "Fourth-Order Time-Stepping for Stiff PDEs". SIAM Journal of Scientific Computing 26 (4): 1214–1233. doi:10.1137/S1064827502410633.
- Zhuang, Hao; Weng, Shih-Hung; Lin, Jeng-Hau; Cheng, Chung-Kuan (2014). MATEX: A Distributed Framework for Transient Simulation of Power Distribution Networks. (PDF). ACM/IEEE Proceedings of The 51st Annual Design Automation Conference (DAC). doi:10.1145/2593069.2593160.
External links
| ||||||||||||||

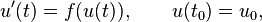
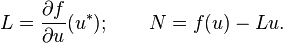
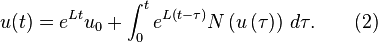
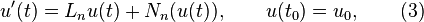
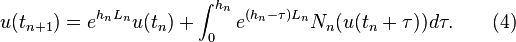
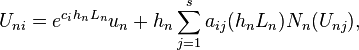
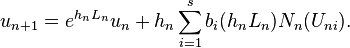
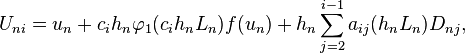
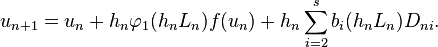
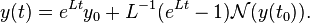
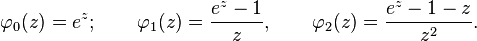
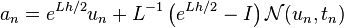
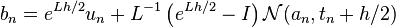
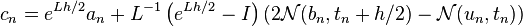
![u_{n+1} = e^{L h} u_n + h^{-2} L^{-3} \left\{
\left[ -4 - Lh + e^{Lh} \left( 4 - 3 L h + (L h)^2 \right) \right] \mathcal{N}( u_n, t_n ) +
2 \left[ 2 + L h + e^{Lh} \left( -2 + L h \right) \right] \left( \mathcal{N}( a_n, t_n+h/2 ) + \mathcal{N}( b_n, t_n + h / 2 ) \right) +
\left[ -4 - 3L h - (Lh)^2 + e^{Lh} \left(4 - Lh \right) \right] \mathcal{N}( c_n, t_n + h )
\right\}.](../I/m/37e1ab1603f323e064b02c9ae741d110.png)