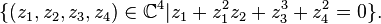Exotic affine space

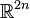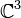In algebraic geometry, an exotic affine space is a complex algebraic variety that is diffeomorphic to $\mathbb{R}^{2n}$ for some n, but is not isomorphic as an algebraic variety to $\mathbb{C}^n$ .^[1]^[2]^[3] An example of an exotic $\mathbb C^3$ is the Koras–Russell cubic threefold,^[4] which is the subset of 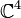$\mathbb C^4$ defined by the polynomial equation

\{(z_1,z_2,z_3,z_4)\in\mathbb C^4|z_1+z_1^2z_2+z_3^3+z_4^2=0\}.

References

↑ Snow, Dennis (2004), "The role of exotic affine spaces in the classification of homogeneous affine varieties", Algebraic Transformation Groups and Algebraic Varieties: Proceedings of the Conference Interesting Algebraic Varieties Arising in Algebraic Transformation Group Theory Held at the Erwin Schrödinger Institute, Vienna, October 22-26, 2001, Encyclopaedia of Mathematical Sciences 132, Berlin: Springer, pp. 169–175, doi:10.1007/978-3-662-05652-3_9, MR 2090674 .
↑ Freudenburg, G.; Russell, P. (2005), "Open problems in affine algebraic geometry", Affine algebraic geometry, Contemporary Mathematics 369, Providence, RI: American Mathematical Society, pp. 1–30, doi:10.1090/conm/369/06801, MR 2126651 .
↑ Zaidenberg, Mikhail (1995-06-02). "On exotic algebraic structures on affine spaces". arXiv:alg-geom/9506005.
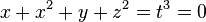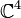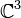↑ L Makar-Limanov (1996), "On the hypersurface $x+x^2+y+z^2=t^3=0$ in $\mathbb C^4$ or a $\mathbb C^3$ -like threefold which is not 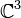$\mathbb C^3$ ", Israel J Math 96: 419–429

This article is issued from Wikipedia - version of the Tuesday, October 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.