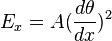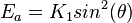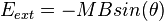Exchange spring magnet

An Exchange Spring Magnet is a magnetic material with high coercivity and high saturation properties derived from the exchange interaction between a hard magnetic material and a soft magnetic material, respectively. Coehoorn et al. were the first able to observe an actual exchange spring magnet.^[1] Exchange Spring Magnets are cheaper than many magnets containing rare earth/transition metals (RE-TM Magnets), as the hard phase of the magnet (which commonly comprises RE-TM material) can be less than 15% of the overall magnet by volume.^[2]

Principle

First proposed by Kneller and Hawig in 1991, the exchange spring magnet utilizes the epitaxy between hard and soft magnetic materials: the hard material helps retain the soft material’s anisotropy, which increases its coercivity.^[2]

The magnetic hysteresis loop of an Exchange Spring Magnet theoretically takes on a shape resembling that of a summation of its hard and soft magnetic components (as seen in Figure 1), meaning its energy product is higher than those of its components. A magnet’s maximum energy product (BH)_max, which is roughly proportional to its coercivity (H_C) and magnetization saturation (M_sat), is used as a metric of its ability to do magnetic work as (BH)_max is twice the magnet’s available magnetostatic energy.^[3] The Exchange Spring Magnet offers a geometry able to improve upon the previously reported maximum energy products of materials such as Rare Earth/Transition Metal complexes; while both materials have sufficiently large H_C values and operate at relatively high Curie Temperatures, the Exchange Spring Magnet can achieve much higher M_sat values than the Rare Earth/Transition Metal (RE-TM) complexes.^[4]

An important component of Exchange Spring Magnets is anisotropy: while exchange spring magnets that are isotropic in bulk still exhibit a greater energy product than many RE-TM magnets, the energy product of their anisotropic form is theorized to be significantly higher.^[3]

Magnetic Energy

Exchange energy

The magnetic moment of a bulk material is the sum of all of its atomic moments. The atomic moments' interactions with each other and with the externally applied field determine the behavior of the magnet. Each atomic magnetic moment tries to orient itself so that the total magnetic energy reaches a minimum. There are generally four types of energy competing with each other to reach equilibrium: each is derived from the exchange coupling effect, magnetic anisotropy, the magnetiostatic energy of the magnet, and the magnet's interaction with external field.

Figure 2: Four types of magnetic energy. Magnetic moments of small groups of atoms are represented by arrows.

Exchange coupling is a quantum mechanical effect that keeps the adjacent moments aligned with one another. Exchange energy of adjacent moments increases as the angle between the two moments increases.

E_x = A (\frac{d\theta}{dx})^2

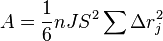where $A=\frac{1}{6}nJS^2\sum \Delta r_j^2$ is the exchange constant and 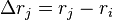$\Delta r_j=r_j-r_i$ is the position vector of neighbor 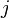$j$ with respect to site $i$ . Typical values of $A$ are on the order of 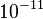$10^{-11}$ J/m.

Anisotropy energy

Magnetic anisotropy energy arises from the crystalline structure of the material. For a simple case, the effect can be modeled by a uniaxial energy distribution. Along an axial direction, called the easy axis, the magnetic moments tend to align. The energy increases if the orientation of a magnetic moment deviates from the easy axis.

E_a = K_1 sin^2(\theta)

Magnetostatic energy

The magnetostatic energy is the energy stored in the field generated by a material's magnetic moments. The magnet's field reaches its maximum intensity if all the magnetic moments orient in one direction; this is what occurs in a hard magnet. In order to prevent building up the magnetic field, sometimes magnetic moments tend to form loops. That way, the energy stored in the magnetic field can be constrained; this is what occurs in a soft magnet. What determines whether a magnet is hard or soft is the dominant term of its magnetic energy. For hard magnets, the anisotropy constant is relatively large, making the magnetic moments align with easy axis. The opposite case applies to soft magnets, in which the magnetostatic energy is dominant.

Another magnetostatic energy arises interaction with an external field. Magnetic moments naturally try to align with the applied field.

E_{ext} = -MBsin(\theta)

Since the magnetostatic energy dominates in the soft magnet, the magnetic moments tend to successfully orient along the external field.

Exchange spring magnet

In the exchange spring magnet, the hard phase has high coercivity and the soft phase has high saturation. The hard phase and the soft phase interact through their interface by exchange coupling.

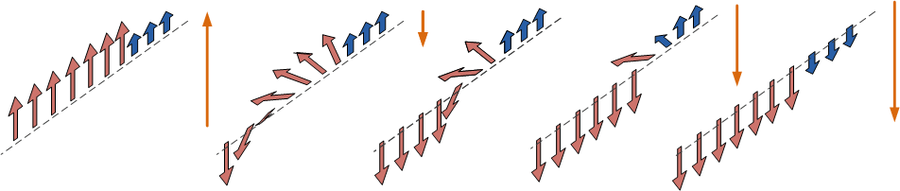
Figure 3: Magnetic moments at the interface of a hard magnetic material and a soft magnetic material. Assumes a one-dimensional: blue arrows stand for the magnetic moments in the hard phase, and red arrows stand for those in soft phase. The length of the arrow shows its magnetization and its width shows its coercivity. The easy axis is assumed to be in the vertical direction.

From left to right in Figure 3, an external field is first applied in an upward direction in order to saturate the magnet. Then, the external field is reversed and starts to demagnetize the magnet. Since the coercivity of the hard phase is relatively high, the moments remain unchanged so as to minimize the anisotropy and exchange energy. The magnetic moments in the soft phase start rotating to align with the applied field.^[5] Because of the exchange coupling at the soft/hard interface, the magnetic moments at the soft phase boundary have to align with the adjacent moment in hard phase. At the regions close to the interface, because of exchange coupling, the chain of magnetic moments acts like a spring. If the external field is increased, more moments in soft phase rotate downward, and the width of the transition region becomes smaller as the exchange energy density increases. The magnetic moments in the hard phase do not rotate until the external field is high enough that the exchange energy density in the transition region is comparable to the anisotropy energy density in the hard phase. At this point, the rotation of magnetic moments in the soft phase starts to affect the hard phase. As the external field surpasses the hard material's coercivity, the hard magnet gets fully demagnetized.

In the previous process, when the magnetic moments in the hard magnet start to rotate, the intensity of external field is already much higher than the coercivity of the soft phase, but there is still a transition region in soft phase. If the thickness of the soft phase is less than twice as thick as the transition region, the soft phase should have a large effective coercivity, smaller than but comparable to the coercivity of the hard phase.

Figure 4: Magnetic moments around thin soft phase

In a thin soft phase, it is hard for the external field to rotate the magnetic moments, similar to a hard magnet with high saturation magnetization. After applying a high external field to partially demagnetize the magnetic moments in the hard phase and after subsequently removing the external field, the rotated moments in the soft phase can be rotated back by exchange coupling with the hard phase (Figure 5). This phenomenon is shown in the hysteresis loop of an exchange spring magnet (Figure 6).

Figure 5: Magnetic moments of an exchange spring magnet upon introducing and removing a relatively large external magnetic field.

Figure 6: Demagnetization curves^[5] of an exchange spring magnet.

Comparing the exchange spring magnet's hysteresis loop with that of a conventional hard magnet demonstrates that the exchange spring magnet is more likely to recover from the opposing external field. When the external field is removed, the remanent magnetization can recover to a value close to its original. The name "exchange spring magnet" is derived from the reversibility of magnetization.^[2]

The dimension of the soft phase inside the exchange spring magnet should be kept small enough so as to retain reversible magnetization. Additionally, the volume fraction of the soft phase needs to be as large as possible in order to achieve a high magnetization saturation. One viable material geometry is to fabricate a magnet by embedding hard particles inside a soft matrix. That way, the soft matrix material occupies the largest volume fraction while being close to the hard particles. The size and spacing of the hard particles is on the scale of nanometers. If the hard magnets are spheres on an fcc space lattice in the soft magnetic phase, the volume fraction of the hard phase can be 9%. Since the total magnetization saturation is summed up by volume fraction, it is close to the value of a pure soft phase.

Fabrication

The fabrication of an Exchange Spring Magnet requires precise control of the particle-matrix structure at the nanometer-scale dimension. Several approaches have been tested, including metallurgical method, sputtering, and particle self-assembly.

Particle Self-Assembly - 4 nm Fe₃O₄ nanoparticles and 4 nm Fe₅₈Pt₄₂ nanoparticles dispersed in solution were deposited as compact structures through self-assembly by evaporating the solution. Then, through annealing, a FePt-Fe₃Pt nanocomposite magnet was formed. The energy density increased from 117 kJ/m³ of the single phase Fe₅₈Pt₄₂ to 160 kJ/m³ of FePt-Fe₃Pt nanocomposite.^[6]
Sputtering - Sm and Co were co-sputtered from elemental targets using a DC Magnetron, onto a Cr(211) buffer on MgO(110) substrates to create Sm₂Co₇. An Fe layer was deposited at 300 - 400 ^oC and capped with Cr.^[7]
Annealing - Multilayers of Fe and Pt were sputtered from elemental targets onto glass. Varying layer composition and annealing conditions were found to alter magnetic properties of final material.^[8]

References

↑ Coehoorn, R.; de Mooij, D.B.;De Waard, C. (1989). "Meltspun permanent magnet materials containing Fe₃B as the main phase" Journal of Magnetism and Magnetic Materials 80 (1) 101-104. doi:10.1016/0304-8853(89)90333-8
1 2 3 Kneller, E. F.; Hawig, R. (July 1991). "The exchange-spring magnet: a new material principle for permanent magnets". IEEE Transactions on Magnetics 27 (4): 3588–3560. Bibcode:1991ITM....27.3588K. doi:10.1109/20.102931.
1 2 Fullerton, E.E.; Jiang, J.S.; Bader, S.D. (1999) "Hard/Soft magnetic heterostructures: model exchange-spring magnets". Journal of Magnetism and Magnetic Materials 200 (1-3) 392-404. doi:10.1016/S0304-8853(99)00376-5
↑ Coey, J.M.D; Skomski, R. (1993). "New Magnets from Interstitial Intermetallics". Physica Scripta T49A: 315-321.
1 2 Monteiro, Pedro M. S.; Schmool, D. S. (June 2010). "Magnetization dynamics in exchange-coupled spring systems with perpendicular anisotropy". Physical Review B 81 (21). arXiv:0911.4137. Bibcode:2010PhRvB..81u4439M. doi:10.1103/PhysRevB.81.214439.
↑ Zeng, Hao; Li, Jing; Liu, J. P.; Wang, Zhong L.; Sun, Shouheng (28 November 2002). "Exchange-coupled nanocomposite magnets by nanoparticle self-assembly". Nature 420 (6914): 395–398. Bibcode:2002Natur.420..395Z. doi:10.1038/nature01208.
↑ Davies, J.E.; Hellwig, O.; Fullerton, E.E.; Jiang, J.S.; Bader, S.D.; Zimányi, G.T.; Liu, K. (2005). "Anisotropy dependence of irreversible switching in Fe ∕ Sm Co and Fe Ni ∕ Fe Pt exchange spring magnet films". Applied Physics Letters 86: 262503. DOI:10.1063/1.1954898
↑ Liu, J.P.; Luo, C.P.; Liu, Y.; Sellmyer, D.J. (1998). "High energy products in rapidly annealed nanoscale Fe/Pt multilayers". Applied Physics Letters 72: 483-485. DOI:10.1063/1.120793

This article is issued from Wikipedia - version of the Saturday, December 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.