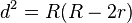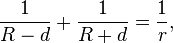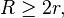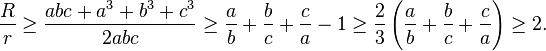Euler's theorem in geometry

In geometry, Euler's theorem states that the distance d between the circumcentre and incentre of a triangle can be expressed as[1][2][3][4]

d^2=R (R-2r) \,

or equivalently

\frac{1}{R-d} + \frac{1}{R+d} = \frac{1}{r},

where R and r denote the circumradius and inradius respectively (the radii of the circumscribed circle and inscribed circle respectively). The theorem is named for Leonhard Euler, who published it in 1767.[5] However, the same result was published earlier by William Chapple in 1746.[6]

From the theorem follows the Euler inequality:[2][3]

R \ge 2r,

which holds with equality only in the equilateral case.[7]:p. 198

Proof

Proof of Euler's theorem in geometry

Letting O be the circumcentre of triangle ABC, and I be its incentre, the extension of AI intersects the circumcircle at L. Then L is the midpoint of arc BC. Join LO and extend it so that it intersects the circumcircle at M. From I construct a perpendicular to AB, and let D be its foot, so ID = r. It is not difficult to prove that triangle ADI is similar to triangle MBL, so ID / BL = AI / ML, i.e. ID × ML = AI × BL. Therefore 2Rr = AI × BL. Join BI. Because

∠ BIL = ∠ A / 2 + ∠ ABC / 2,
∠ IBL = ∠ ABC / 2 + ∠ CBL = ∠ ABC / 2 + ∠ A / 2,

we have ∠ BIL = ∠ IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q; then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d2 = R(R − 2r).

Stronger version of the inequality

A stronger version[7]:p. 198 is

\frac{R}{r} \geq \frac{abc+a^3+b^3+c^3}{2abc} \geq \frac{a}{b}+\frac{b}{c}+\frac{c}{a}-1 \geq \frac{2}{3} \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \right) \geq 2.

See also

References

  1. ↑ Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover Publ., p. 186.
  2. 1 2 Alsina, Claudi; Nelsen, Roger (2009), When Less is More: Visualizing Basic Inequalities, Dolciani Mathematical Expositions 36, Mathematical Association of America, p. 56, ISBN 9780883853429.
  3. 1 2 Debnath, Lokenath (2010), The Legacy of Leonhard Euler: A Tricentennial Tribute, World Scientific, p. 124, ISBN 9781848165250.
  4. ↑ Dunham, William (2007), The Genius of Euler: Reflections on his Life and Work, Spectrum Series 2, Mathematical Association of America, p. 300, ISBN 9780883855584.
  5. ↑ Euler, Leonhard (1767), "Solutio facilis problematum quorumdam geometricorum difficillimorum" (PDF), Novi Commentarii academiae scientiarum Petropolitanae (in Latin) 11: 103–123.
  6. ↑ Chapple, William (1746), "An essay on the properties of triangles inscribed in and circumscribed about two given circles", Miscellanea Curiosa Mathematica 4: 117–124. The formula for the distance is near the bottom of p.123.
  7. 1 2 Svrtan, Dragutin; Veljan, Darko (2012), "Non-Euclidean versions of some classical triangle inequalities", Forum Geometricorum 12: 197–209.

External links

Wikimedia Commons has media related to Euler's theorem in geometry.
This article is issued from Wikipedia - version of the Monday, August 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.