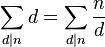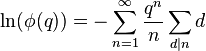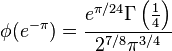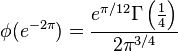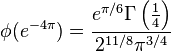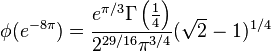Euler function
- For other meanings, see List of topics named after Leonhard Euler.
In mathematics, the Euler function is given by
Named after Leonhard Euler, it is a prototypical example of a q-series, a modular form, and provides the prototypical example of a relation between combinatorics and complex analysis.
Properties
The coefficient  in the formal power series expansion for
in the formal power series expansion for 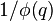 gives the number of all partitions of k. That is,
gives the number of all partitions of k. That is,
where  is the partition function of k.
is the partition function of k.
The Euler identity, also known as the Pentagonal number theorem is
Note that 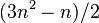 is a pentagonal number.
is a pentagonal number.
The Euler function is related to the Dedekind eta function through a Ramanujan identity as
where 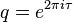 is the square of the nome.
is the square of the nome.
Note that both functions have the symmetry of the modular group.
The Euler function may be expressed as a Q-Pochhammer symbol:
The logarithm of the Euler function is the sum of the logarithms in the product expression, each of which may be expanded about q=0, yielding:
which is a Lambert series with coefficients -1/n. The logarithm of the Euler function may therefore be expressed as:
where
On account of the following identity,
this may also be written as
Special values
The next identities come from Ramanujan's lost notebook, Part V, p. 326.
References
- Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001



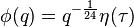
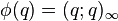
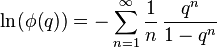
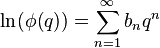
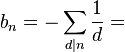 -[1/1, 3/2, 4/3, 7/4, 6/5, 12/6, 8/7, 15/8, 13/9, 18/10, ...] (see
-[1/1, 3/2, 4/3, 7/4, 6/5, 12/6, 8/7, 15/8, 13/9, 18/10, ...] (see