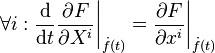Euler–Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation,[1] or Lagrange's equation (although the latter name is ambiguous—see disambiguation page), is a second-order partial differential equation whose solutions are the functions for which a given functional is stationary. It was developed by Swiss-Russian mathematician Leonhard Euler and French-Italian mathematician Joseph-Louis Lagrange in the 1750s.
Because a differentiable functional is stationary at its local maxima and minima, the Euler–Lagrange equation is useful for solving optimization problems in which, given some functional, one seeks the function minimizing (or maximizing) it. This is analogous to Fermat's theorem in calculus, stating that at any point where a differentiable function attains a local extremum, its derivative is zero.
In Lagrangian mechanics, because of Hamilton's principle of stationary action, the evolution of a physical system is described by the solutions to the Euler–Lagrange equation for the action of the system. In classical mechanics, it is equivalent to Newton's laws of motion, but it has the advantage that it takes the same form in any system of generalized coordinates, and it is better suited to generalizations. In classical field theory there is an analogous equation to calculate the dynamics of a field.
History
The Euler–Lagrange equation was developed in the 1750s by Euler and Lagrange in connection with their studies of the tautochrone problem. This is the problem of determining a curve on which a weighted particle will fall to a fixed point in a fixed amount of time, independent of the starting point.
Lagrange solved this problem in 1755 and sent the solution to Euler. Both further developed Lagrange's method and applied it to mechanics, which led to the formulation of Lagrangian mechanics. Their correspondence ultimately led to the calculus of variations, a term coined by Euler himself in 1766.[2]
Statement
The Euler–Lagrange equation is an equation satisfied by a function, q, of a real argument, t, which is a stationary point of the functional
where:
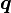 is the function to be found:
is the function to be found:
![\begin{align}
\boldsymbol q \colon [a, b] \subset \mathbb{R} & \to X \\
t & \mapsto x = \boldsymbol q(t)
\end{align}](../I/m/718c98f1521dc8b9006db27c24b72ac6.png)
- such that
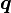 is differentiable,
is differentiable, 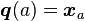 , and
, and 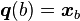 ;
;
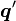 ; is the derivative of
; is the derivative of 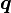 :
:
- TX being the tangent bundle of X defined by
-
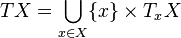 ;
;
- L is a real-valued function with continuous first partial derivatives:
The Euler–Lagrange equation, then, is given by
where Lx and Lv denote the partial derivatives of L with respect to the second and third arguments, respectively.
If the dimension of the space X is greater than 1, this is a system of differential equations, one for each component:
Derivation of one-dimensional Euler–Lagrange equation The derivation of the one-dimensional Euler–Lagrange equation is one of the classic proofs in mathematics. It relies on the fundamental lemma of calculus of variations.
We wish to find a function
 which satisfies the boundary conditions
which satisfies the boundary conditions 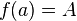 ,
, 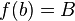 , and which extremizes the functional
, and which extremizes the functionalWe assume that
 is twice continuously differentiable.[3] A weaker assumption can be used, but the proof becomes more difficult.
is twice continuously differentiable.[3] A weaker assumption can be used, but the proof becomes more difficult.If
 extremizes the functional subject to the boundary conditions, then any slight perturbation of
extremizes the functional subject to the boundary conditions, then any slight perturbation of  that preserves the boundary values must either increase
that preserves the boundary values must either increase 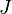 (if
(if  is a minimizer) or decrease
is a minimizer) or decrease 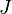 (if
(if  is a maximizer).
is a maximizer). Let
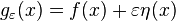 be the result of such a perturbation
be the result of such a perturbation 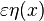 of
of  , where
, where  is small and
is small and 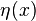 is a differentiable function satisfying
is a differentiable function satisfying 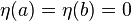 . Then define
. Then definewhere
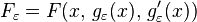 .
.We now wish to calculate the total derivative of
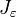 with respect to ε.
with respect to ε.It follows from the total derivative that
So
When ε = 0 we have gε = f, Fε = F(x, f(x), f'(x)) and Jε has an extremum value, so that
The next step is to use integration by parts on the second term of the integrand, yielding
Using the boundary conditions
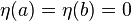 ,
, Applying the fundamental lemma of calculus of variations now yields the Euler–Lagrange equation
-
Alternate derivation of one-dimensional Euler–Lagrange equation Given a functional
on
![C^1([a, b])](../I/m/8a33eba68d7379b365730528445287cb.png) with the boundary conditions
with the boundary conditions 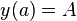 and
and 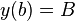 , we proceed by approximating the extremal curve by a polygonal line with
, we proceed by approximating the extremal curve by a polygonal line with  segments and passing to the limit as the number of segments grows arbitrarily large.
segments and passing to the limit as the number of segments grows arbitrarily large.Divide the interval
![[a, b]](../I/m/2c3d331bc98b44e71cb2aae9edadca7e.png) into
into  equal segments with endpoints
equal segments with endpoints 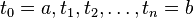 and let
and let 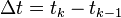 . Rather than a smooth function
. Rather than a smooth function  we consider the polygonal line with vertices
we consider the polygonal line with vertices 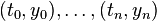 , where
, where 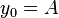 and
and 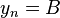 . Accordingly, our functional becomes a real function of
. Accordingly, our functional becomes a real function of  variables given by
variables given byExtremals of this new functional defined on the discrete points
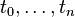 correspond to points where
correspond to points whereEvaluating this partial derivative gives
Dividing the above equation by
 gives
givesand taking the limit as
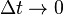 of the right-hand side of this expression yields
of the right-hand side of this expression yieldsThe left hand side of the previous equation is the functional derivative
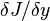 of the functional
of the functional 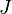 . A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
. A necessary condition for a differentiable functional to have an extremum on some function is that its functional derivative at that function vanishes, which is granted by the last equation.
Examples
A standard example is finding the real-valued function on the interval [a, b], such that f(a) = c and f(b) = d, the length of whose graph is as short as possible. The length of the graph of f is:
the integrand function being L(x, y, y′) = √1 + y′ ² evaluated at (x, y, y′) = (x, f(x), f′(x)).
The partial derivatives of L are:
By substituting these into the Euler–Lagrange equation, we obtain
that is, the function must have constant first derivative, and thus its graph is a straight line.
Variations for several functions, several variables, and higher derivatives
Single function of single variable with higher derivatives
The stationary values of the functional
can be obtained from the Euler–Lagrange equation[4]
under fixed boundary conditions for the function itself as well as for the first  derivatives (i.e. for all
derivatives (i.e. for all 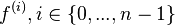 ). The endpoint values of the highest derivative
). The endpoint values of the highest derivative  remain flexible.
remain flexible.
Several functions of one variable
If the problem involves finding several functions (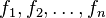 ) of a single independent variable (
) of a single independent variable ( ) that define an extremum of the functional
) that define an extremum of the functional
then the corresponding Euler–Lagrange equations are[5]
Single function of several variables
A multi-dimensional generalization comes from considering a function on n variables. If Ω is some surface, then
is extremized only if f satisfies the partial differential equation
When n = 2 and  is the energy functional, this leads to the soap-film minimal surface problem.
is the energy functional, this leads to the soap-film minimal surface problem.
Several functions of several variables
If there are several unknown functions to be determined and several variables such that
the system of Euler–Lagrange equations is[4]
Single function of two variables with higher derivatives
If there is a single unknown function f to be determined that is dependent on two variables x1 and x2 and if the functional depends on higher derivatives of f up to n-th order such that
then the Euler–Lagrange equation is[4]
which can be represented shortly as:
where 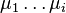 are indices that span the number of variables, that is they go from 1 to 2. Here summation over the
are indices that span the number of variables, that is they go from 1 to 2. Here summation over the 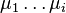 indices is implied according to Einstein notation.
indices is implied according to Einstein notation.
Several functions of several variables with higher derivatives
If there is are p unknown functions fi to be determined that are dependent on m variables x1 ... xm and if the functional depends on higher derivatives of the fi up to n-th order such that
where 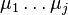 are indices that span the number of variables, that is they go from 1 to m. Then the Euler–Lagrange equation is
are indices that span the number of variables, that is they go from 1 to m. Then the Euler–Lagrange equation is
where summation over the 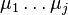 is implied according to Einstein notation. This can be expressed more compactly as
is implied according to Einstein notation. This can be expressed more compactly as
Generalization to Manifolds
Let  be a smooth manifold, and let
be a smooth manifold, and let ![C^\infty([a,b])](../I/m/d6f5b42d28035b0d623cf73269112975.png) denote the space of smooth functions
denote the space of smooth functions ![f:[a,b]\to M](../I/m/8f1ff4d53fdaf8318624191e885e9094.png) . Then, for functionals
. Then, for functionals ![S:C^\infty ([a,b])\to \mathbb{R}](../I/m/69fe2a0b06f1b668113bb37a3b7f4257.png) of the form
of the form
where 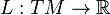 is the Lagrangian, the statement
is the Lagrangian, the statement 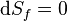 is equivalent to the statement that, for all
is equivalent to the statement that, for all ![t\in [a,b]](../I/m/c9ef8c742260828c469822e9c5dbe2c9.png) , each coordinate frame trivialization
, each coordinate frame trivialization 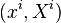 of a neighborhood of
of a neighborhood of 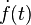 yields the following
yields the following 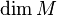 equations:
equations:
See also
| Look up Euler–Lagrange equation in Wiktionary, the free dictionary. |
- Lagrangian mechanics
- Hamiltonian mechanics
- Analytical mechanics
- Beltrami identity
- Functional derivative
Notes
- ↑ Fox, Charles (1987). An introduction to the calculus of variations. Courier Dover Publications. ISBN 978-0-486-65499-7.
- ↑ A short biography of Lagrange
- ↑ Courant & Hilbert 1953, p. 184
- 1 2 3 Courant, R; Hilbert, D (1953). Methods of Mathematical Physics. Vol. I (First English ed.). New York: Interscience Publishers, Inc. ISBN 978-0471504474.
- ↑ Weinstock, R., 1952, Calculus of Variations With Applications to Physics and Engineering, McGraw-Hill Book Company, New York.
References
- Hazewinkel, Michiel, ed. (2001), "Lagrange equations (in mechanics)", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Euler-Lagrange Differential Equation", MathWorld.
- Calculus of Variations at PlanetMath.org.
- Gelfand, Izrail Moiseevich (1963). Calculus of Variations. Dover. ISBN 0-486-41448-5.
- Roubicek, T.: Calculus of variations. Chap.17 in: Mathematical Tools for Physicists. (Ed. M. Grinfeld) J. Wiley, Weinheim, 2014, ISBN 978-3-527-41188-7, pp.551-588.
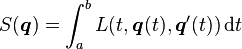
![\begin{align}
q' \colon [a, b] & \to T_{q(t)}X \\
t & \mapsto v = q'(t)
\end{align}](../I/m/6eacf3691f5c195a7be14edd1e08256a.png)
![\begin{align}
L \colon [a, b] \times TX & \to \mathbb{R} \\
(t, x, v) & \mapsto L(t, x, v).
\end{align}](../I/m/54bebfb32c57b34e20889c07b59d37f0.png)
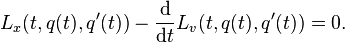
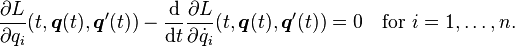
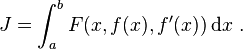
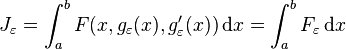
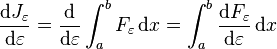
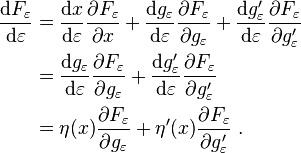
![\frac{\mathrm{d} J_\varepsilon}{\mathrm{d} \varepsilon} = \int_a^b \left[\eta(x) \frac{\partial F_\varepsilon}{\partial g_\varepsilon} + \eta'(x) \frac{\partial F_\varepsilon}{\partial g_\varepsilon'} \, \right]\,\mathrm{d}x \ .](../I/m/c2294204d520d4683c117c673e4154d2.png)
![\frac{\mathrm d J_\varepsilon}{\mathrm d\varepsilon}\bigg|_{\varepsilon=0} = \int_a^b \left[ \eta(x) \frac{\partial F}{\partial f} + \eta'(x) \frac{\partial F}{\partial f'} \,\right]\,\mathrm{d}x = 0 \ .](../I/m/d93e82d24f887e82ca3ad9ad17bde0a6.png)
![\int_a^b \left[ \frac{\partial F}{\partial f} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial f'} \right] \eta(x)\,\mathrm{d}x + \left[ \eta(x) \frac{\partial F}{\partial f'} \right]_a^b = 0 \ .](../I/m/e3f166868be48daff25a996cc96e4211.png)
![\int_a^b \left[ \frac{\partial F}{\partial f} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial F}{\partial f'} \right] \eta(x)\,\mathrm{d}x = 0 \ . \,\!](../I/m/6bfde7a643d46649a23c5514c2ebb6db.png)
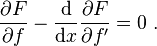
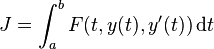
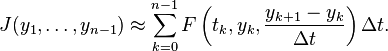
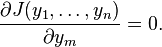
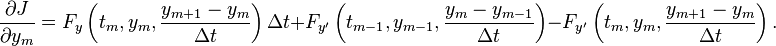
![\frac{\partial J}{\partial y_m \Delta t} = F_y\left(t_m, y_m, \frac{y_{m + 1} - y_m}{\Delta t}\right) - \frac{1}{\Delta t}\left[F_{y'}\left(t_m, y_m, \frac{y_{m + 1} - y_m}{\Delta t}\right) - F_{y'}\left(t_{m - 1}, y_{m - 1}, \frac{y_m - y_{m - 1}}{\Delta t}\right)\right],](../I/m/9f23d8e27c7fe3f2e39b37dc16150762.png)
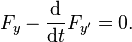
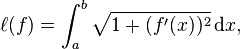
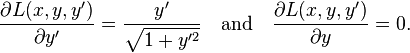
![I[f] = \int_{x_0}^{x_1} \mathcal{L}(x, f, f', f'', \dots, f^{(n)})~\mathrm{d}x ~;~~
f' := \cfrac{\mathrm{d}f}{\mathrm{d}x}, ~f'' := \cfrac{\mathrm{d}^2f}{\mathrm{d}x^2}, ~
f^{(n)} := \cfrac{\mathrm{d}^nf}{\mathrm{d}x^n}](../I/m/a502eb7022b03884d406d6f5ef622df6.png)
![I[f_1,f_2, \dots, f_n] = \int_{x_0}^{x_1} \mathcal{L}(x, f_1, f_2, \dots, f_n, f_1', f_2', \dots, f_n')~\mathrm{d}x
~;~~ f_i' := \cfrac{\mathrm{d}f_i}{\mathrm{d}x}](../I/m/fd54c9b17a87e46c0c24e2e1dc3db939.png)
![I[f] = \int_{\Omega} \mathcal{L}(x_1, \dots , x_n, f, f_{x_1}, \dots , f_{x_n})\, \mathrm{d}\mathbf{x}\,\! ~;~~
f_{x_i} := \cfrac{\partial f}{\partial x_i}](../I/m/be771dae942a49056cbd7a514103b4b4.png)
![I[f_1,f_2,\dots,f_m] = \int_{\Omega} \mathcal{L}(x_1, \dots , x_n, f_1, \dots, f_m, f_{1,1}, \dots , f_{1,n}, \dots, f_{m,1}, \dots, f_{m,n}) \, \mathrm{d}\mathbf{x}\,\! ~;~~
f_{j,i} := \cfrac{\partial f_j}{\partial x_i}](../I/m/4fe6b0cb4e2680092795c3f23f6970d7.png)
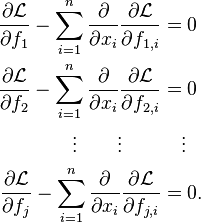
![\begin{align}
I[f] & = \int_{\Omega} \mathcal{L}(x_1, x_2, f, f_{,1}, f_{,2}, f_{,11}, f_{,12}, f_{,22},
\dots, f_{,22\dots 2})\, \mathrm{d}\mathbf{x} \\
& \qquad \quad
f_{,i} := \cfrac{\partial f}{\partial x_i} \; , \quad
f_{,ij} := \cfrac{\partial^2 f}{\partial x_i\partial x_j} \; , \;\; \dots
\end{align}](../I/m/471886a0dd261c4eb989ac279fcb1028.png)
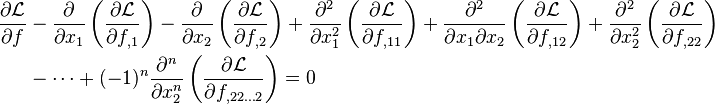
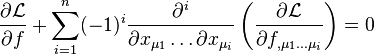
![\begin{align}
I[f_1,\ldots,f_p] & = \int_{\Omega} \mathcal{L}(x_1, \ldots, x_m; f_1,\ldots,f_p; f_{1,1},\ldots,
f_{p,m}; f_{1,11},\ldots, f_{p,mm};\ldots; f_{p,m\ldots m})\, \mathrm{d}\mathbf{x} \\
& \qquad \quad
f_{i,\mu} := \cfrac{\partial f_i}{\partial x_\mu} \; , \quad
f_{i,\mu_1\mu_2} := \cfrac{\partial^2 f_i}{\partial x_{\mu_1}\partial x_{\mu_2}} \; , \;\; \dots
\end{align}](../I/m/2192db6e4670f125383ad20a06131f15.png)
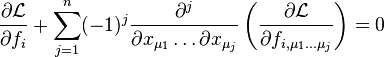
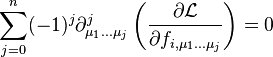
![S[f]=\int_a^b (L\circ\dot{f})(t)\,\mathrm{d} t](../I/m/42d370f5d970b2fdc4f0e39df2dc2319.png)