Euclidean field

This article is about ordered fields. For algebraic number fields whose ring of integers has a Euclidean algorithm, see Norm-Euclidean field. For the class of models in statistical mechanics, see Euclidean field theory.

In mathematics, a Euclidean field is an ordered field K for which every non-negative element is a square: that is, x ≥ 0 in K implies that x = y² for some y in K.

Properties

Every Euclidean field is an ordered Pythagorean field, but the converse is not true.^[1]
If E/F is a finite extension, and E is Euclidean, then so is F. This "going-down theorem" is a consequence of the Diller–Dress theorem.^[2]

Examples

The real numbers R with the usual operations and ordering form a Euclidean field.
The field of real algebraic numbers 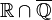$\mathbb{R}\cap\mathbb{\overline Q}$ is a Euclidean field.
The real constructible numbers, those (signed) lengths which can be constructed from a rational segment by ruler and compass constructions, form a Euclidean field.^[3]
The field of hyperreal numbers is a Euclidean field.

Counterexamples

The rational numbers Q with the usual operations and ordering do not form a Euclidean field. For example, 2 is not a square in Q since the square root of 2 is irrational.^[4] By the going-down result above, no algebraic number field can be Euclidean.^[2]
The complex numbers C do not form a Euclidean field since they cannot be given the structure of an ordered field.

Euclidean closure

The Euclidean closure of an ordered field K is an extension of K in the quadratic closure of K which is maximal with respect to being an ordered field with an order extending that of K.^[5]

References

↑ Martin (1998) p. 89
1 2 Lam (2005) p.270
↑ Martin (1998) pp. 35–36
↑ Martin (1998) p. 35
↑ Efrat (2006) p. 177

Efrat, Ido (2006). Valuations, orderings, and Milnor K-theory. Mathematical Surveys and Monographs 124. Providence, RI: American Mathematical Society. ISBN 0-8218-4041-X. Zbl 1103.12002.
Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.
Martin, George E. (1998). Geometric Constructions. Undergraduate Texts in Mathematics. Springer-Verlag. ISBN 0-387-98276-0. Zbl 0890.51015.

External links

Euclidean Field at PlanetMath.org.

This article is issued from Wikipedia - version of the Thursday, August 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.