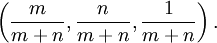Euclid's orchard

One corner of Euclid's orchard, in which trees are labelled with the x co-ordinate of their projection on the plane x+y=1.

In mathematics, informally speaking, Euclid's orchard is an array of one-dimensional "trees" of unit height planted at the lattice points in one quadrant of a square lattice.[1] More formally, Euclid's orchard is the set of line segments from (i, j, 0) to (i, j, 1) where i and j are positive integers.

Plan view of one corner of Euclid's orchard. Trees marked by a solid blue dot are visible from the origin.
Perspective view of Euclid's orchard from the origin. Red trees denote rows two off the main diagonal.

The trees visible from the origin are those at lattice points (m, n, 0) where m and n are coprime, i.e., where the fraction m⁄n is in reduced form. The name Euclid's orchard is derived from the Euclidean algorithm.

If the orchard is projected relative to the origin onto the plane x+y=1 (or, equivalently, drawn in perspective from a viewpoint at the origin) the tops of the trees form a graph of Thomae's function. The point (m, n, 1) projects to

\left ( \frac {m}{m+n}, \frac {n}{m+n}, \frac {1}{m+n} \right ).

See also

References

  1. ↑ Weisstein, Eric W., "Euclid's Orchard", MathWorld.

External links

This article is issued from Wikipedia - version of the Monday, July 21, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.