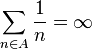Erdős conjecture on arithmetic progressions
Erdős' conjecture on arithmetic progressions, often referred to as the Erdős–Turán conjecture, is a conjecture in arithmetic combinatorics (not to be confused with the Erdős–Turán conjecture on additive bases). It states that if the sum of the reciprocals of the members of a set A of positive integers diverges, then A contains arbitrarily long arithmetic progressions.
Formally, the conjecture states that if
then A contains arithmetic progressions of any given length. (Sets satisfying the hypothesis are called large sets.)
History
In 1936, Erdős and Turán made the weaker conjecture that any set of integers with positive natural density contains infinitely many 3 term arithmetic progressions.[1] This was proven by Klaus Roth in 1952, and generalized to arbitrarily long arithmetic progressions by Szemerédi in 1975 in what is now known as Szemerédi's theorem.
In a 1976 talk titled "To the memory of my lifelong friend and collaborator Paul Turán," Paul Erdős offered a prize of US$3000 for a proof of this conjecture.[2] The problem is currently worth US$5000.[3]
Progress and related results
| | Unsolved problem in mathematics: Does every large set contain arbitrarily long arithmetic progressions? (more unsolved problems in mathematics) |
Erdős' conjecture on arithmetic progressions can be viewed as a stronger version of Szemerédi's theorem. Because the sum of the reciprocals of the primes diverges, the Green–Tao theorem on arithmetic progressions is a special case of the conjecture.
Even the weaker claim that A must contain at least one arithmetic progression of length 3 is open. The strongest related result is due to Bloom.[4]
The converse of the conjecture is not true. For example, the set {1, 10, 11, 100, 101, 102, 1000, 1001, 1002, 1003, 10000, ...} contains arithmetic progressions of every finite length, but the sum of the reciprocals of its elements converges.
See also
References
- ↑ Erdős, Paul; Turán, Paul (1936), "On some sequences of integers" (PDF), Journal of the London Mathematical Society 11 (4): 261–264, doi:10.1112/jlms/s1-11.4.261.
- ↑ Problems in number theory and Combinatorics, in Proceedings of the Sixth Manitoba Conference on Numerical Mathematics (Univ. Manitoba, Winnipeg, Man., 1976), Congress. Numer. XVIII, 35–58, Utilitas Math., Winnipeg, Man., 1977
- ↑ p. 354, Soifer, Alexander (2008); The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators; New York: Springer. ISBN 978-0-387-74640-1
- ↑ Bloom, Thomas F. (2014). "A quantitative improvement for Roth's theorem on arithmetic progressions". arXiv:1405.5800.
- P. Erdős: Résultats et problèmes en théorie de nombres, Séminaire Delange-Pisot-Poitou (14e année: 1972/1973), Théorie des nombres, Fasc 2., Exp. No. 24, pp. 7,
- P. Erdős and P.Turán, On some sequences of integers, J. London Math. Soc. 11 (1936), 261–264.
- P. Erdős: Problems in number theory and combinatorics, Proc. Sixth Manitoba Conf. on Num. Math., Congress Numer. XVIII(1977), 35–58.
- P. Erdős: On the combinatorial problems which I would most like to see solved, Combinatorica, 1(1981), 28. doi:10.1007/BF02579174
External links
- The Erdős–Turán conjecture or the Erdős conjecture? on MathOverflow