Equivariant bundle

In differential geometry, given a compact Lie group G, an equivariant bundle is a fiber bundle such that the total space and the base spaces are both G-spaces and the projection map 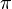$\pi$ between them is equivariant: $\pi \circ g = g \circ \pi$ with some extra requirement depending on a typical fiber.

For example, an equivariant vector bundle is an equivariant bundle.

References

Berline, Nicole; Getzler, E.; Vergne, Michèle (2004), Heat Kernels and Dirac Operators, Berlin, New York: Springer-Verlag

This article is issued from Wikipedia - version of the Wednesday, November 12, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.