Equisatisfiability

In logic, two formulae are equisatisfiable if the first formula is satisfiable whenever the second is and vice versa; in other words, either both formulae are satisfiable or both are not. Two equisatisfiable formulae may have different models, provided they both have some or both have none. As a result, equisatisfiability is different from logical equivalence, as two equivalent formulae always have the same models.

Equisatisfiability is generally used in the context of translating formulae, so that one can define a translation to be correct if the original and resulting formulae are equisatisfiable. Examples of translations involving this concept are Skolemization and some translations into conjunctive normal form.

Examples

A translation from propositional logic into propositional logic in which every binary disjunction 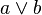$a \vee b$ is replaced by $((a \vee n) \wedge (\neg n \vee b))$ , where $n$ is a new variable (one for each replaced disjunction) is a transformation in which satisfiability is preserved: the original and resulting formulae are equisatisfiable. Note that these two formulae are not equivalent: the first formula has the model in which $b$ is true while $a$ and $n$ are false, and this is not a model of the second formula, in which $n$ has to be true in this case.

This article is issued from Wikipedia - version of the Tuesday, April 16, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.