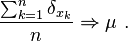Equidistributed sequence
In mathematics, a sequence {s1, s2, s3, ...} of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that interval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration.
Definition
A sequence {s1, s2, s3, ...} of real numbers is said to be equidistributed on a non-degenerate interval [a, b] if for any subinterval [c, d] of [a, b] we have
(Here, the notation |{s1,...,sn }∩[c,d]| denotes the number of elements, out of the first n elements of the sequence, that are between c and d.)
For example, if a sequence is equidistributed in [0, 2], since the interval [0.5, 0.9] occupies 1/5 of the length of the interval [0, 2], as n becomes large, the proportion of the first n members of the sequence which fall between 0.5 and 0.9 must approach 1/5. Loosely speaking, one could say that each member of the sequence is equally likely to fall anywhere in its range. However, this is not to say that {sn} is a sequence of random variables; rather, it is a determinate sequence of real numbers.
Discrepancy
We define the discrepancy DN for a sequence {s1, s2, s3, ...} with respect to the interval [a, b] as
A sequence is thus equidistributed if the discrepancy DN tends to zero as N tends to infinity.
Equidistribution is a rather weak criterion to express the fact that a sequence fills the segment leaving no gaps. For example, the drawings of a random variable uniform over a segment will be equidistributed in the segment, but there will be large gaps compared to a sequence which first enumerates multiples of ε in the segment, for some small ε, in an appropriately chosen way, and then continues to do this for smaller and smaller values of ε. See low-discrepancy sequence for stronger criteria and constructions of low-discrepancy sequences for constructions of sequences which are more evenly distributed.
Riemann integral criterion for equidistribution
Recall that if f is a function having a Riemann integral in the interval [a, b], then its integral is the limit of Riemann sums taken by sampling the function f in a set of points chosen from a fine partition of the interval. Therefore, if some sequence is equidistributed in [a, b], it is expected that this sequence can be used to calculate the integral of a Riemann-integrable function. This leads to the following criterion[1] for an equidistributed sequence:
Suppose {s1, s2, s3, ...} is a sequence contained in the interval [a, b]. Then the following conditions are equivalent:
- The sequence is equidistributed on [a, b].
- For every Riemann-integrable (complex-valued) function f : [a, b] → C, the following limit holds:
Proof First note that the definition of an equidistributed sequence is equivalent to the integral criterion whenever f is the indicator function of an interval: If f = 1[c, d], then the left hand side is the proportion of points of the sequence falling in the interval [c, d], and the right hand side is exactly 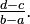
This means 2 → 1 (since indicator functions are Riemann-integrable), and 1 → 2 for f being an indicator function of an interval. It remains to assume that the integral criterion holds for indicator functions and prove that it holds for general Riemann-integrable functions as well.
Note that both sides of the integral criterion equation are linear in f, and therefore the criterion holds for linear combinations of interval indicators, that is, step functions.
To show it holds for f being a general Riemann-integrable function, first assume f is real-valued. Then by using Darboux's definition of the integral, we have for every ε > 0 two step functions f1 and f2 such that f1 ≤ f ≤ f2 and
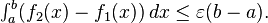 Notice that:
Notice that:By subtracting, we see that the limit superior and limit inferior of
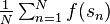 differ by at most ε. Since ε is arbitrary, we have the existence of the limit, and by Darboux's definition of the integral, it is the correct limit.
differ by at most ε. Since ε is arbitrary, we have the existence of the limit, and by Darboux's definition of the integral, it is the correct limit.Finally, for complex-valued Riemann-integrable functions, the result follows again from linearity, and from the fact that every such function can be written as f = u + vi, where u, v are real-valued and Riemann-integrable. ∎
This criterion leads to the idea of Monte-Carlo integration, where integrals are computed by sampling the function over a sequence of random variables equidistributed in the interval.
It is not possible to generalize the integral criterion to a class of functions bigger than just the Riemann-integrable ones. For example, if the Lebesgue integral is considered and f is taken to be in L1, then this criterion fails. As a counterexample, take f to be the indicator function of some equidistributed sequence. Then in the criterion, the left hand side is always 1, whereas the right hand side is zero, because the sequence is countable, so f is zero almost everywhere.
In fact, the de Bruijn–Post Theorem states the converse of the above criterion: If f is a function such that the criterion above holds for any equidistributed sequence in [a, b], then f is Riemann-integrable in [a, b].[2]
Equidistribution modulo 1
A sequence {a1, a2, a3, ...} of real numbers is said to be equidistributed modulo 1 or uniformly distributed modulo 1 if the sequence of the fractional parts of an, denoted by {an} or by an−⌊an⌋, is equidistributed in the interval [0, 1].
Examples

- The equidistribution theorem: The sequence of all multiples of an irrational α,
- 0, α, 2α, 3α, 4α, ...
- is equidistributed modulo 1.[3]
- More generally, if p is a polynomial with at least one irrational coefficient (other than the constant term) then the sequence p(n) is uniformly distributed modulo 1.
This was proven by Weyl and is an application of van der Corput's difference theorem.[4]
- The sequence log(n) is not uniformly distributed modulo 1.[3]
- The sequence of all multiples of an irrational α by successive prime numbers,
- 2α, 3α, 5α, 7α, 11α, ...
- is equidistributed modulo 1. This is a famous theorem of analytic number theory, published by I. M. Vinogradov in 1948.[5]
- The van der Corput sequence is equidistributed.[6]
Weyl's criterion
Weyl's criterion states that the sequence an is equidistributed modulo 1 if and only if for all non-zero integers ℓ,
The criterion is named after, and was first formulated by, Hermann Weyl.[7] It allows to reduce equidistribution questions to bounds on exponential sums, a fundamental and general method.
Sketch of proof If the sequence is equidistributed modulo 1, then we can apply the Riemann integral criterion (described above) on the function 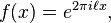 which has integral zero on the interval [0, 1]. This gives Weyl's criterion immediately.
which has integral zero on the interval [0, 1]. This gives Weyl's criterion immediately.
Conversely, suppose Weyl's criterion holds. Then the Riemann integral criterion holds for functions f as above, and by linearity of the criterion, it holds for f being any trigonometric polynomial. By the Stone–Weierstrass theorem and an approximation argument, this extends to any continuous function f.
Finally, let f be the indicator function of an interval. It is possible to bound f from above and below by two continuous functions on the interval, whose integrals differ by an arbitrary ε. By an argument similar to the proof of the Riemann integral criterion, it is possible to extend the result to any interval indicator function f, thereby proving equidistribution modulo 1 of the given sequence. ∎
Generalizations
- A quantitative form of Weyl's criterion is given by the Erdős–Turán inequality.
- Weyl's criterion extends naturally to higher dimensions, assuming the natural generalization of the definition of equidistribution modulo 1:
The sequence vn of vectors in Rk is equidistributed modulo 1 if and only if for any non-zero vector ℓ ∈ Zk,
Example of usage
Weyl's criterion can be used to easily prove the equidistribution theorem, stating that the sequence of multiples 0, α, 2α, 3α, ... of some real number α is equidistributed modulo 1 if and only if α is irrational.[3]
Suppose α is irrational and denote our sequence by aj = jα (where j starts from 0, to simplify the formula later). Let ℓ ≠ 0 be an integer. Since α is irrational, ℓα can never be an integer, so 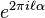 can never be 1. Using the formula for the sum of a finite geometric series,
can never be 1. Using the formula for the sum of a finite geometric series,
a bound that does not depend on n. Therefore after dividing by n and letting n tend to infinity, the left hand side tends to zero, and Weyl's criterion is satisfied.
Conversely, notice that if α is rational then this sequence is not equidistributed modulo 1, because there is only a finite number of options for the fractional part of aj = jα.
van der Corput's difference theorem
A theorem of Johannes van der Corput[8] states that if for each h the sequence sn+h − sn is uniformly distributed modulo 1, then so is sn.[9][10][11]
A van der Corput set is a set H of integers such that if for each h in H the sequence sn+h − sn is uniformly distributed modulo 1, then so is sn.[10][11]
Metric theorems
Metric theorems describe the behaviour of a parametrised sequence for almost all values of some parameter α: that is, for values of α not lying in some exceptional set of Lebesgue measure zero.
- For any sequence of distinct integers bn, the sequence {bnα} is equidistributed mod 1 for almost all values of α.[12]
- The sequence {αn} is equidistributed mod 1 for almost all values of α > 1.[13]
It is not known whether the sequences {en} or {πn} are equidistributed mod 1. However it is known that the sequence {αn} is not equidistributed mod 1 if α is a PV number.
Well-distributed sequence
A sequence {s1, s2, s3, ...} of real numbers is said to be well-distributed on [a, b] if for any subinterval [c, d] of [a, b] we have
uniformly in k. Clearly every well-distributed sequence is uniformly distributed, but the converse does not hold. The definition of well-distributed modulo 1 is analogous.
Sequences equidistributed with respect to an arbitrary measure
For an arbitrary probability measure space 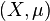 , a sequence of points
, a sequence of points 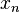 is said to be equidistributed with respect to
is said to be equidistributed with respect to  if the mean of point measures converges weakly to
if the mean of point measures converges weakly to  :[14]
:[14]
It is true, for example, that for any Borel probability measure on a separable, metrizable space, there exists an equidistributed sequence (with respect to the measure).
See also
References
- ↑ Kuipers & Niederreiter (2006) pp. 2–3
- ↑ http://math.uga.edu/~pete/udnotes.pdf, Theorem 8
- 1 2 3 Kuipers & Niederreiter (2006) p. 8
- ↑ Kuipers & Niederreiter (2006) p. 27
- ↑ Kuipers & Niederreiter (2006) p. 129
- ↑ Kuipers & Niederreiter (2006) p. 127
- ↑ Weyl, H. (1916). "Ueber die Gleichverteilung von Zahlen mod. Eins,". Math. Ann. 77 (3): 313–352. doi:10.1007/BF01475864.
- ↑ van der Corput, J. (1931), "Diophantische Ungleichungen. I. Zur Gleichverteilung Modulo Eins", Acta Mathematica (Springer Netherlands) 56: 373–456, doi:10.1007/BF02545780, ISSN 0001-5962, JFM 57.0230.05, Zbl 0001.20102
- ↑ Kuipers & Niederreiter (2006) p. 26
- 1 2 Montgomery (1994) p.18
- 1 2 Montgomery, Hugh L. (2001). "Harmonic analysis as found in analytic number theory". In Byrnes, James S. Twentieth century harmonic analysis–a celebration. Proceedings of the NATO Advanced Study Institute, Il Ciocco, Italy, July 2–15, 2000. NATO Sci. Ser. II, Math. Phys. Chem. 33. Dordrecht: Kluwer Academic Publishers. pp. 271–293. Zbl 1001.11001.
- ↑ See Bernstein, Felix (1911), "Über eine Anwendung der Mengenlehre auf ein aus der Theorie der säkularen Störungen herrührendes Problem", Mathematische Annalen 71 (3): 417–439, doi:10.1007/BF01456856.
- ↑ Koksma, J. F. (1935), "Ein mengentheoretischer Satz über die Gleichverteilung modulo Eins", Compositio Mathematica 2: 250–258, JFM 61.0205.01, Zbl 0012.01401
- ↑ Kuipers & Niederreiter (2006) p.171
- Kuipers, L.; Niederreiter, H. (2006) [1974]. Uniform Distribution of Sequences. Dover Publishing. ISBN 0-486-45019-8.
- Kuipers, L.; Niederreiter, H. (1974). Uniform Distribution of Sequences. John Wiley & Sons Inc. ISBN 0-471-51045-9. Zbl 0281.10001.
- Montgomery, Hugh L. (1994). Ten lectures on the interface between analytic number theory and harmonic analysis. Regional Conference Series in Mathematics 84. Providence, RI: American Mathematical Society. ISBN 0-8218-0737-4. Zbl 0814.11001.
Further reading
- Granville, Andrew; Rudnick, Zeév, eds. (2007). Equidistribution in number theory, an introduction. Proceedings of the NATO Advanced Study Institute on equidistribution in number theory, Montréal, Canada, July 11–22, 2005. NATO Science Series II: Mathematics, Physics and Chemistry 237. Dordrecht: Springer-Verlag. ISBN 978-1-4020-5403-7. Zbl 1121.11004.
- Tao, Terence (2012). Higher order Fourier analysis. Graduate Studies in Mathematics 142. Providence, RI: American Mathematical Society. ISBN 978-0-8218-8986-2. Zbl pre06110460.
External links
- Weisstein, Eric W., "Equidistributed Sequence", MathWorld.
- Weisstein, Eric W., "Weyl's Criterion", MathWorld.
- Weyl's Criterion at PlanetMath.org.
- Lecture notes with proof of Weyl's Criterion
![\lim_{n\to\infty}{ \left|\{\,s_1,\dots,s_n \,\} \cap [c,d] \right| \over n}={d-c \over b-a} . \,](../I/m/cefbaaedc02643bfe0c760249c43753e.png)
![D_N = \sup_{a\le c\le d\le b} \left\vert \frac{\left|\{\,s_1,\dots,s_N \,\} \cap [c,d] \right|}{N} - \frac{d-c}{b-a} \right\vert . \,](../I/m/1c2ae8b113b8f282eca24a9c1fe29a94.png)
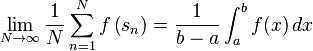
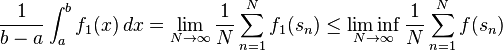
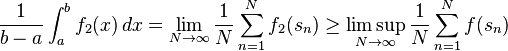
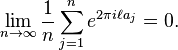
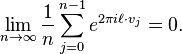
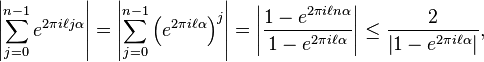
![\lim_{n\to\infty}{ \left|\{\,s_{k+1},\dots,s_{k+n} \,\} \cap [c,d] \right| \over n}={d-c \over b-a} \,](../I/m/95cdac6073216610e334abc71cfe53ca.png)