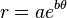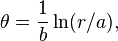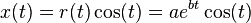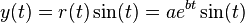Logarithmic spiral
 Logarithmic spiral (pitch 10°) |
 Cutaway of a nautilus shell showing the chambers arranged in an approximately logarithmic spiral. The plotted spiral (dashed blue curve) is based on growth rate parameter b = 0.1759. |
 Romanesco broccoli, which grows in a logarithmic spiral |
 A section of the Mandelbrot set following a logarithmic spiral |
 An extratropical cyclone over Iceland shows an approximately logarithmic spiral pattern |
 The arms of spiral galaxies often have the shape of a logarithmic spiral, here the Whirlpool Galaxy |
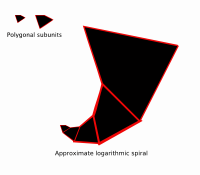 Polygon spiral |
A logarithmic spiral, equiangular spiral or growth spiral is a self-similar spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral".
Definition
In polar coordinates 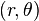 the logarithmic curve can be written as[1]
the logarithmic curve can be written as[1]
or
with  being the base of natural logarithms, and
being the base of natural logarithms, and  and
and  being arbitrary positive real constants.
being arbitrary positive real constants.
In parametric form, the curve is
with real numbers  and
and  .
.
The spiral has the property that the angle φ between the tangent and radial line at the point 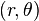 is constant. This property can be expressed in differential geometric terms as
is constant. This property can be expressed in differential geometric terms as
The derivative of 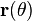 is proportional to the parameter
is proportional to the parameter  . In other words, it controls how "tightly" and in which direction the spiral spirals. In the extreme case that
. In other words, it controls how "tightly" and in which direction the spiral spirals. In the extreme case that  (
(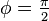 ) the spiral becomes a circle of radius
) the spiral becomes a circle of radius  . Conversely, in the limit that
. Conversely, in the limit that  approaches infinity (φ → 0) the spiral tends toward a straight half-line. The complement of φ is called the pitch.
approaches infinity (φ → 0) the spiral tends toward a straight half-line. The complement of φ is called the pitch.
Spira mirabilis and Jacob Bernoulli
Spira mirabilis, Latin for "miraculous spiral", is another name for the logarithmic spiral. Although this curve had already been named by other mathematicians, the specific name ("miraculous" or "marvelous" spiral) was given to this curve by Jacob Bernoulli, because he was fascinated by one of its unique mathematical properties: the size of the spiral increases but its shape is unaltered with each successive curve, a property known as self-similarity. Possibly as a result of this unique property, the spira mirabilis has evolved in nature, appearing in certain growing forms such as nautilus shells and sunflower heads. Jacob Bernoulli wanted such a spiral engraved on his headstone along with the phrase "Eadem mutata resurgo" ("Although changed, I shall arise the same."), but, by error, an Archimedean spiral was placed there instead.[2][3]
Properties
The logarithmic spiral can be distinguished from the Archimedean spiral by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression, while in an Archimedean spiral these distances are constant.
Logarithmic spirals are self-similar in that the result of applying any similarity transformation to the spiral is congruent to the original untransformed spiral. Scaling by a factor 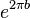 , where b is the parameter from the definition of the spiral, with the center of scaling at the origin, gives the same curve as the original; other scale factors give a curve that is rotated from the original position of the spiral. Logarithmic spirals are also congruent to their own involutes, evolutes, and the pedal curves based on their centers.
, where b is the parameter from the definition of the spiral, with the center of scaling at the origin, gives the same curve as the original; other scale factors give a curve that is rotated from the original position of the spiral. Logarithmic spirals are also congruent to their own involutes, evolutes, and the pedal curves based on their centers.
Starting at a point  and moving inward along the spiral, one can circle the origin an unbounded number of times without reaching it; yet, the total distance covered on this path is finite; that is, the limit as
and moving inward along the spiral, one can circle the origin an unbounded number of times without reaching it; yet, the total distance covered on this path is finite; that is, the limit as  goes toward
goes toward 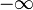 is finite. This property was first realized by Evangelista Torricelli even before calculus had been invented.[4]
The total distance covered is
is finite. This property was first realized by Evangelista Torricelli even before calculus had been invented.[4]
The total distance covered is 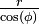 , where
, where  is the straight-line distance from
is the straight-line distance from  to the origin.
to the origin.
The exponential function exactly maps all lines not parallel with the real or imaginary axis in the complex plane, to all logarithmic spirals in the complex plane with centre at 0. (Up to adding integer multiples of 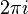 to the lines, the mapping of all lines to all logarithmic spirals is onto.) The pitch angle of the logarithmic spiral is the angle between the line and the imaginary axis.
to the lines, the mapping of all lines to all logarithmic spirals is onto.) The pitch angle of the logarithmic spiral is the angle between the line and the imaginary axis.
The function 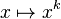 , where the constant
, where the constant  is a complex number with non-zero imaginary part, maps the real line to a logarithmic spiral in the complex plane.
is a complex number with non-zero imaginary part, maps the real line to a logarithmic spiral in the complex plane.
The golden spiral is a logarithmic spiral that grows outward by a factor of the golden ratio for every 90 degrees of rotation (pitch about 17.03239 degrees). It can be approximated by a "Fibonacci spiral", made of a sequence of quarter circles with radii proportional to Fibonacci numbers.
Logarithmic spirals in nature
In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follows some examples and reasons:
- The approach of a hawk to its prey. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.[5]
- The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the sun (or moon for nocturnal species) is the only light source and flying that way will result in a practically straight line.[6]
- The arms of spiral galaxies.[7] Our own galaxy, the Milky Way, has several spiral arms, each of which is roughly a logarithmic spiral with pitch of about 12 degrees.[8]
- The nerves of the cornea (this is, corneal nerves of the subepithelial layer terminate near superficial epithelial layer of the cornea in a logarithmic spiral pattern).[9]
- The bands of tropical cyclones, such as hurricanes.[10]
- Many biological structures including the shells of mollusks.[11] In these cases, the reason may be construction from expanding similar shapes, as shown for polygonal figures in the accompanying graphic.
- Logarithmic spiral beaches can form as the result of wave refraction and diffraction by the coast. Half Moon Bay (California) is an example of such a type of beach.[12]
See also
References
- ↑ Priya Hemenway (2005). Divine Proportion: Φ Phi in Art, Nature, and Science. Sterling Publishing Co. ISBN 1-4027-3522-7.
- ↑ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ↑ Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Evolutes." p. 206
- ↑ Carl Benjamin Boyer (1949). The history of the calculus and its conceptual development. Courier Dover Publications. p. 133. ISBN 978-0-486-60509-8.
- ↑ Chin, Gilbert J. (8 December 2000), "Organismal Biology: Flying Along a Logarithmic Spiral", Science 290 (5498): 1857, doi:10.1126/science.290.5498.1857c
- ↑ John Himmelman (2002). Discovering Moths: Nighttime Jewels in Your Own Backyard. Down East Enterprise Inc. p. 63. ISBN 978-0-89272-528-1.
- ↑ G. Bertin and C. C. Lin (1996). Spiral structure in galaxies: a density wave theory. MIT Press. p. 78. ISBN 978-0-262-02396-2.
- ↑ David J. Darling (2004). The universal book of mathematics: from Abracadabra to Zeno's paradoxes. John Wiley and Sons. p. 188. ISBN 978-0-471-27047-8.
- ↑ C. Q. Yu CQ and M. I. Rosenblatt, "Transgenic corneal neurofluorescence in mice: a new model for in vivo investigation of nerve structure and regeneration," Invest Ophthalmol Vis Sci. 2007 Apr;48(4):1535-42.
- ↑ Andrew Gray (1901). Treatise on physics, Volume 1. Churchill. pp. 356–357.
- ↑ Michael Cortie (1992). "The form, function, and synthesis of the molluscan shell". In István Hargittai and Clifford A. Pickover. Spiral symmetry. World Scientific. p. 370. ISBN 978-981-02-0615-4.
- ↑ Allan Thomas Williams and Anton Micallef (2009). Beach management: principles and practice. Earthscan. p. 14. ISBN 978-1-84407-435-8.
- Weisstein, Eric W., "Logarithmic Spiral", MathWorld.
- Jim Wilson, Equiangular Spiral (or Logarithmic Spiral) and Its Related Curves, University of Georgia (1999)
- Alexander Bogomolny, Spira Mirabilis - Wonderful Spiral, at cut-the-knot
External links
| Wikimedia Commons has media related to Logarithmic spirals. |
- Spira mirabilis history and math
- Astronomy Picture of the Day, Hurricane Isabel vs. the Whirlpool Galaxy
- Astronomy Picture of the Day, Typhoon Rammasun vs. the Pinwheel Galaxy
- SpiralZoom.com, an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
- Online exploration using JSXGraph (JavaScript)