Enumerations of specific permutation classes
In the study of permutation patterns, there has been considerable interest in enumerating specific permutation classes, especially those with relatively few basis elements.
Classes avoiding one pattern of length 3
There are two symmetry classes and a single Wilf class for single permutations of length three.
| β | sequence enumerating Avn(β) | OEIS | type of sequence | exact enumeration reference |
|---|---|---|---|---|
|
123 |
1, 2, 5, 14, 42, 132, 429, 1430, ... | A000108 | algebraic (nonrational) g.f. Catalan numbers | MacMahon (1915/16) Knuth (1968) |
Classes avoiding one pattern of length 4
There are seven symmetry classes and three Wilf classes for single permutations of length four.
| β | sequence enumerating Avn(β) | OEIS | type of sequence | exact enumeration reference |
|---|---|---|---|---|
|
1342 |
1, 2, 6, 23, 103, 512, 2740, 15485, ... | A022558 | algebraic (nonrational) g.f. | Bóna (1997) |
|
1234 |
1, 2, 6, 23, 103, 513, 2761, 15767, ... | A005802 | holonomic (nonalgebraic) g.f. | Gessel (1990) |
| 1324 | 1, 2, 6, 23, 103, 513, 2762, 15793, ... | A061552 |
No non-recursive formula counting 1324-avoiding permutations is known. A recursive formula was given by Marinov & Radoičić (2003). A more efficient algorithm using functional equations was given by Johansson & Nakamura (2014), which was enhanced by Conway & Guttmann (2015). Bevan (2015) has provided a lower bound and Bóna (2015) an upper bound for the growth of this class.
Classes avoiding two patterns of length 3
There are five symmetry classes and three Wilf classes, all of which were enumerated in Simion & Schmidt (1985).
| B | sequence enumerating Avn(B) | OEIS | type of sequence |
|---|---|---|---|
| 123, 321 | 1, 2, 4, 4, 0, 0, 0, 0, ... | n/a | finite |
| 123, 231 | 1, 2, 4, 7, 11, 16, 22, 29, ... | A000124 | polynomial, 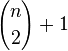 |
|
123, 132 |
1, 2, 4, 8, 16, 32, 64, 128, ... | A000079 | rational g.f.,  |
Classes avoiding one pattern of length 3 and one of length 4
There are eighteen symmetry classes and nine Wilf classes, all of which have been enumerated. For these results, see Atkinson (1999) or West (1996).
| B | sequence enumerating Avn(B) | OEIS | type of sequence |
|---|---|---|---|
| 321, 1234 | 1, 2, 5, 13, 25, 25, 0, 0, ... | n/a | finite |
| 321, 2134 | 1, 2, 5, 13, 30, 61, 112, 190, ... | A116699 | polynomial |
| 132, 4321 | 1, 2, 5, 13, 31, 66, 127, 225, ... | A116701 | polynomial |
| 321, 1324 | 1, 2, 5, 13, 32, 72, 148, 281, ... | A179257 | polynomial |
| 321, 1342 | 1, 2, 5, 13, 32, 74, 163, 347, ... | A116702 | rational g.f. |
| 321, 2143 | 1, 2, 5, 13, 33, 80, 185, 411, ... | A088921 | rational g.f. |
|
132, 4312 |
1, 2, 5, 13, 33, 81, 193, 449, ... | A005183 | rational g.f. |
| 132, 3214 | 1, 2, 5, 13, 33, 82, 202, 497, ... | A116703 | rational g.f. |
|
321, 2341 |
1, 2, 5, 13, 34, 89, 233, 610, ... | A001519 | rational g.f., alternate Fibonacci numbers |
Classes avoiding two patterns of length 4
There are 56 symmetry classes and 38 Wilf equivalence classes, of which 30 have been enumerated.
| B | sequence enumerating Avn(B) | OEIS | type of sequence | exact enumeration reference |
|---|---|---|---|---|
| 4321, 1234 | 1, 2, 6, 22, 86, 306, 882, 1764, ... | A206736 | finite | Erdős–Szekeres theorem |
| 4312, 1234 | 1, 2, 6, 22, 86, 321, 1085, 3266, ... | A116705 | polynomial | Kremer & Shiu (2003) |
| 4321, 3124 | 1, 2, 6, 22, 86, 330, 1198, 4087, ... | A116708 | rational g.f. | Kremer & Shiu (2003) |
| 4312, 2134 | 1, 2, 6, 22, 86, 330, 1206, 4174, ... | A116706 | rational g.f. | Kremer & Shiu (2003) |
| 4321, 1324 | 1, 2, 6, 22, 86, 332, 1217, 4140, ... | A165524 | polynomial | Vatter (2012) |
| 4321, 2143 | 1, 2, 6, 22, 86, 333, 1235, 4339, ... | A165525 | rational g.f. | Albert, Atkinson & Brignall (2012) |
| 4312, 1324 | 1, 2, 6, 22, 86, 335, 1266, 4598, ... | A165526 | rational g.f. | Albert, Atkinson & Brignall (2012) |
| 4231, 2143 | 1, 2, 6, 22, 86, 335, 1271, 4680, ... | A165527 | rational g.f. | Albert, Atkinson & Brignall (2011) |
| 4231, 1324 | 1, 2, 6, 22, 86, 336, 1282, 4758, ... | A165528 | rational g.f. | Albert, Atkinson & Vatter (2009) |
| 4213, 2341 | 1, 2, 6, 22, 86, 336, 1290, 4870, ... | A116709 | rational g.f. | Kremer & Shiu (2003) |
| 4312, 2143 | 1, 2, 6, 22, 86, 337, 1295, 4854, ... | A165529 | rational g.f. | Albert, Atkinson & Brignall (2012) |
| 4213, 1243 | 1, 2, 6, 22, 86, 337, 1299, 4910, ... | A116710 | rational g.f. | Kremer & Shiu (2003) |
| 4321, 3142 | 1, 2, 6, 22, 86, 338, 1314, 5046, ... | A165530 | rational g.f. | Vatter (2012) |
| 4213, 1342 | 1, 2, 6, 22, 86, 338, 1318, 5106, ... | A116707 | rational g.f. | Kremer & Shiu (2003) |
| 4312, 2341 | 1, 2, 6, 22, 86, 338, 1318, 5110, ... | A116704 | rational g.f. | Kremer & Shiu (2003) |
| 3412, 2143 | 1, 2, 6, 22, 86, 340, 1340, 5254, ... | A029759 | algebraic (nonrational) g.f. | Atkinson (1998) |
|
4321, 4123 |
1, 2, 6, 22, 86, 342, 1366, 5462, ... | A047849 | rational g.f. | Kremer & Shiu (2003) |
| 4123, 2341 | 1, 2, 6, 22, 87, 348, 1374, 5335, ... | A165531 | algebraic (nonrational) g.f. | Atkinson, Sagan & Vatter (2012) |
| 4231, 3214 | 1, 2, 6, 22, 87, 352, 1428, 5768, ... | A165532 | ||
| 4213, 1432 | 1, 2, 6, 22, 87, 352, 1434, 5861, ... | A165533 | ||
|
4312, 3421 |
1, 2, 6, 22, 87, 354, 1459, 6056, ... | A164651 | algebraic (nonrational) g.f. | Callan (preprint1) determined the enumeration; Le (2005) established the Wilf-equivalence. |
| 4312, 3124 | 1, 2, 6, 22, 88, 363, 1507, 6241, ... | A165534 | algebraic (nonrational) g.f. | Pantone (preprint) |
| 4231, 3124 | 1, 2, 6, 22, 88, 363, 1508, 6255, ... | A165535 | algebraic (nonrational) g.f. | Albert, Atkinson & Vatter (2014) |
| 4312, 3214 | 1, 2, 6, 22, 88, 365, 1540, 6568, ... | A165536 | ||
|
4231, 3412 |
1, 2, 6, 22, 88, 366, 1552, 6652, ... | A032351 | algebraic (nonrational) g.f. | Bóna (1998) |
| 4213, 2143 | 1, 2, 6, 22, 88, 366, 1556, 6720, ... | A165537 | algebraic (nonrational) g.f. | Bevan (preprint2) |
| 4312, 3142 | 1, 2, 6, 22, 88, 367, 1568, 6810, ... | A165538 | algebraic (nonrational) g.f. | Albert, Atkinson & Vatter (2014) |
| 4213, 3421 | 1, 2, 6, 22, 88, 367, 1571, 6861, ... | A165539 | algebraic (nonrational) g.f. | Bevan (preprint1) |
|
4213, 3412 |
1, 2, 6, 22, 88, 368, 1584, 6968, ... | A109033 | algebraic (nonrational) g.f. | Le (2005) |
| 4321, 3214 | 1, 2, 6, 22, 89, 376, 1611, 6901, ... | A165540 | algebraic (nonrational) g.f. | Bevan (preprint1) |
| 4213, 3142 | 1, 2, 6, 22, 89, 379, 1664, 7460, ... | A165541 | algebraic (nonrational) g.f. | Albert, Atkinson & Vatter (2014) |
| 4231, 4123 | 1, 2, 6, 22, 89, 380, 1677, 7566, ... | A165542 | ||
| 4321, 4213 | 1, 2, 6, 22, 89, 380, 1678, 7584, ... | A165543 | algebraic (nonrational) g.f. | Callan (preprint2) |
| 4123, 3412 | 1, 2, 6, 22, 89, 381, 1696, 7781, ... | A165544 | ||
| 4312, 4123 | 1, 2, 6, 22, 89, 382, 1711, 7922, ... | A165545 | ||
|
4321, 4312 |
1, 2, 6, 22, 90, 394, 1806, 8558, ... | A006318 | algebraic (nonrational) g.f. Schröder numbers | Kremer (2000), Kremer (2003) |
| 3412, 2413 | 1, 2, 6, 22, 90, 395, 1823, 8741, ... | A165546 | ||
| 4321, 4231 | 1, 2, 6, 22, 90, 396, 1837, 8864, ... | A053617 |
External links
The Database of Permutation Pattern Avoidance, maintained by Bridget Tenner, contains details of the enumeration of many other permutation classes with relatively few basis elements.
See also
References
- Albert, Michael H.; Elder, Murray; Rechnitzer, Andrew; Westcott, P.; Zabrocki, Mike (2006), "On the Stanley-Wilf limit of 4231-avoiding permutations and a conjecture of Arratia", Advances in Applied Mathematics 36: 96–105, doi:10.1016/j.aam.2005.05.007, MR 2199982.
- Albert, Michael H.; Atkinson, M. D.; Brignall, Robert (2011), "The enumeration of permutations avoiding 2143 and 4231" (PDF), Pure Mathematics and Applications 22: 87–98.
- Albert, Michael H.; Atkinson, M. D.; Brignall, Robert (2012), "The enumeration of three pattern classes using monotone grid classes", Electronic Journal of Combinatorics 19 (3): P20, 34 pp..
- Albert, Michael H.; Atkinson, M. D.; Vatter, Vincent (2009), "Counting 1324, 4231-avoiding permutations", Electronic Journal of Combinatorics 16 (1): R136, 9 pp., MR 2577304.
- Albert, Michael H.; Atkinson, M. D.; Vatter, Vincent (2014), "Inflations of geometric grid classes: three case studies", Australasian Journal of Combinatorics 58 (1): 27–47.
- Atkinson, M. D. (1998), "Permutations which are the union of an increasing and a decreasing subsequence", Electronic Journal of Combinatorics 5: R6, 13 pp., MR 1490467.
- Atkinson, M. D. (1999), "Restricted permutations", Discrete Mathematics 195: 27–38, doi:10.1016/S0012-365X(98)00162-9, MR 1663866.
- Atkinson, M. D.; Sagan, Bruce E.; Vatter, Vincent (2012), "Counting (3+1)-avoiding permutations", European Journal of Combinatorics 33: 49–61, doi:10.1016/j.ejc.2011.06.006, MR 2854630.
- Bevan, David (2015), "Permutations avoiding 1324 and patterns in Łukasiewicz paths", J. London Math. Soc. 92 (1): 105–122.
- Bevan, David (preprint1), The permutation classes Av(1234,2341) and Av(1243,2314), arXiv:1407.0570 Check date values in:
|date=(help). - Bevan, David (preprint2), The permutation class Av(4213,2143), arXiv:1510.06328 Check date values in:
|date=(help). - Bóna, Miklós (1997), "Exact enumeration of 1342-avoiding permutations: a close link with labeled trees and planar maps", J. Combin. Theory Ser. A 80: 257–272, doi:10.1006/jcta.1997.2800, MR 1485138.
- Bóna, Miklós (1998), "The permutation classes equinumerous to the smooth class", Electronic Journal of Combinatorics 5: R31, 12 pp., MR 1626487.
- Bóna, Miklós (2015), "A new record for 1324-avoiding permutations", European Journal of Combinatorics: 198–206, doi:10.1007/s40879-014-0020-6.
- Callan, David (preprint1), The number of 1243, 2134-avoiding permutations, arXiv:1303.3857 Check date values in:
|date=(help). - Callan, David (preprint2), Permutations avoiding 4321 and 3241 have an algebraic generating function, arXiv:1306.3193 Check date values in:
|date=(help). - Conway, Andrew; Guttmann, Anthony (2015), "On 1324-avoiding permutations", Adv. in Appl. Math. 64: 50–69.
- Gessel, Ira M. (1990), "Symmetric functions and P-recursiveness", J. Combin. Theory Ser. A 53: 257–285, doi:10.1016/0097-3165(90)90060-A, MR 1041448.
- Johansson, Fredrik; Nakamura, Brian (2014), "Using functional equations to enumerate 1324-avoiding permutations", Adv. in Appl. Math. 56: 20–34.
- Knuth, Donald E. (1968), The Art Of Computer Programming Vol. 1, Boston: Addison-Wesley, ISBN 0-201-89683-4, MR 0286317, OCLC 155842391.
- Kremer, Darla (2000), "Permutations with forbidden subsequences and a generalized Schröder number", Discrete Mathematics 218: 121–130, doi:10.1016/S0012-365X(99)00302-7, MR 1754331.
- Kremer, Darla (2003), "Postscript: “Permutations with forbidden subsequences and a generalized Schröder number”", Discrete Mathematics 270: 333–334, doi:10.1016/S0012-365X(03)00124-9, MR 1997910.
- Kremer, Darla; Shiu, Wai Chee (2003), "Finite transition matrices for permutations avoiding pairs of length four patterns", Discrete Mathematics 268: 171–183, doi:10.1016/S0012-365X(03)00042-6, MR 1983276.
- Le, Ian (2005), "Wilf classes of pairs of permutations of length 4", Electronic Journal of Combinatorics 12: R25, 27 pp., MR 2156679.
- MacMahon, Percy A. (1915/16), Combinatory Analysis, London: Cambridge University Press Check date values in:
|date=(help). - Marinov, Darko; Radoičić, Radoš (2003), "Counting 1324-Avoiding Permutations", Electronic Journal of Combinatorics 9 (2): R13, 9 pp., MR 2028282.
- Pantone, Jay (preprint), The Enumeration of Permutations Avoiding 3124 and 4312, arXiv:1309.0832 Check date values in:
|date=(help). - Simion, Rodica; Schmidt, Frank W. (1985), "Restricted permutations", European Journal of Combinatorics 6: 383–406, doi:10.1016/s0195-6698(85)80052-4, MR 0829358.
- Vatter, Vincent (2012), "Finding regular insertion encodings for permutation classes", Journal of Symbolic Computation 47: 259–265, doi:10.1016/j.jsc.2011.11.002, MR 2869320.
- West, Julian (1996), "Generating trees and forbidden subsequences", Discrete Mathematics 157: 363–374, doi:10.1016/S0012-365X(96)83023-8, MR 1417303.