Engel identity
The Engel identity, named after Friedrich Engel, is a mathematical equation that is satisfied by all elements of a Lie ring, in the case of an Engel Lie ring, or by all the elements of a group, in the case of an Engel group. The Engel identity is the defining condition of an Engel group.
Formal definition
A Lie ring  is defined as a nonassociative ring with multiplication that is anticommutative and satisfies the Jacobi identity with respect to the Lie bracket
is defined as a nonassociative ring with multiplication that is anticommutative and satisfies the Jacobi identity with respect to the Lie bracket ![[x,y]](../I/m/8ca042e8ff30aba99a78e069db08b58a.png) , defined for all elements
, defined for all elements  in the ring
in the ring  . The Lie ring
. The Lie ring  is defined to be an n-Engel Lie ring if and only if
is defined to be an n-Engel Lie ring if and only if
- for all
 in
in  , the n-Engel identity
, the n-Engel identity
![[x,[x, \ldots, [x,[x,y]],\ldots]] = 0](../I/m/ca90347b44312ca3c96cc71e90581bb7.png) (n copies of
(n copies of  ), is satisfied.[1]
), is satisfied.[1]
In the case of a group  , in the preceding definition, use the definition [x,y] = x−1 • y−1 • x • y and replace
, in the preceding definition, use the definition [x,y] = x−1 • y−1 • x • y and replace  by
by 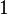 , where
, where 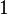 is the identity element of the group
is the identity element of the group  .[2]
.[2]
See also
References
- ↑ Traustason, Gunnar (1993). "Engel Lie-Algebras". Quart. J. Math. Oxford 44 (3): 355–384. doi:10.1093/qmath/44.3.355.
- ↑ Traustason, Gunnar. "Engel groups (a survey)" (PDF).