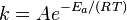Activation energy
In chemistry, activation energy is a term introduced in 1889 by the Swedish scientist Svante Arrhenius to describe the minimum energy which must be available to a chemical system with potential reactants to result in a chemical reaction. Activation energy may also be defined as the minimum energy required to start a chemical reaction. The activation energy of a reaction is usually denoted by Ea and given in units of kilojoules per mole (kJ/mol) or kilocalories per mole (kcal/mol).
Activation energy can be thought of as the height of the potential barrier (sometimes called the energy barrier) separating two minima of potential energy (of the reactants and products of a reaction). For a chemical reaction to proceed at a reasonable rate, there should exist an appreciable number of molecules with translational energy equal to or greater than the activation energy.
At a more advanced level, the Arrhenius Activation energy term from the Arrhenius equation is best regarded as an experimentally determined parameter that indicates the sensitivity of the reaction rate to temperature. There are two objections to associating this activation energy with the threshold barrier for an elementary reaction. First, it is often unclear as to whether or not reaction does proceed in one step; threshold barriers that are averaged out over all elementary steps have little theoretical value. Second, even if the reaction being studied is elementary, a spectrum of individual collisions contributes to rate constants obtained from bulk ('bulb') experiments involving billions of molecules, with many different reactant collision geometries and angles, different translational and (possibly) vibrational energies—all of which may lead to different microscopic reaction rates.
Temperature independence and the relation to the Arrhenius equation
The Arrhenius equation gives the quantitative basis of the relationship between the activation energy and the rate at which a reaction proceeds. From the Arrhenius equation, the activation energy can be found through the relation
where A is the frequency factor for the reaction, R is the universal gas constant, T is the temperature (in kelvin), and k is the reaction rate coefficient. Even without knowing A, Ea can be evaluated from the variation in reaction rate coefficients as a function of temperature (within the validity of the Arrhenius equation).
Negative activation energy
In some cases, rates of reaction decrease with increasing temperature. When following an approximately exponential relationship so the rate constant can still be fit to an Arrhenius expression, this results in a negative value of Ea. Elementary reactions exhibiting these negative activation energies are typically barrierless reactions, in which the reaction proceeding relies on the capture of the molecules in a potential well. Increasing the temperature leads to a reduced probability of the colliding molecules capturing one another (with more glancing collisions not leading to reaction as the higher momentum carries the colliding particles out of the potential well), expressed as a reaction cross section that decreases with increasing temperature. Such a situation no longer leads itself to direct interpretations as the height of a potential spot.
Catalysis
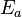) and enthalpy of formation (ΔH) with and without a catalyst, plotted against the reaction coordinate. The highest energy position (peak position) represents the transition state. With the catalyst, the energy required to enter transition state decreases, thereby decreasing the energy required to initiate the reaction.A substance that modifies the transition state to lower the activation energy is termed a catalyst; a biological catalyst is termed an enzyme. It is important to note that a catalyst increases the rate of reaction without being consumed by it. In addition, while the catalyst lowers the activation energy, it does not change the energies of the original reactants or products. Rather, the reactant energy and the product energy remain the same and only the activation energy is altered (lowered).
Relationship with Gibbs energy
In the Arrhenius equation, the term activation energy (Ea) is used to describe the energy required to reach the transition state. Likewise, the Eyring equation is a similar equation that also describes the rate of a reaction. Instead of also using Ea, however, the Eyring equation uses the concept of Gibbs energy and the symbol *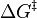
to denote the energy of the transition state. This implies that the equation is similar but not identical to the Arrhenius one, because the Gibbs energy contains an entropic term in addition to the enthalpic one.