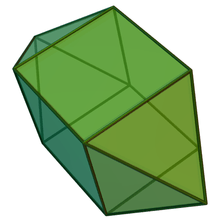
Elongated square bipyramid
| Elongated square bipyramid | |
|---|---|
 | |
| Type |
Johnson J14 - J15 - J16 |
| Faces |
8 triangles 4 squares |
| Edges | 20 |
| Vertices | 10 |
| Vertex configuration |
2(34) 8(32.42) |
| Symmetry group | D4h, [4,2], (*422) |
| Rotation group | D4, [4,2]+, (422) |
| Dual polyhedron | Square bifrustum |
| Properties | convex |
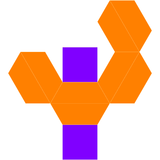
| Net | |
 | |
In geometry, the elongated square bipyramid is one of the Johnson solids (J15). As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves.
It has been named the pencil cube due to its shape.[1]
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[2]
A zircon crystal is an example of an elongated square bipyramid.
Dual polyhedron
The dual of the elongated square bipyramid is called a square bifrustum and has 10 faces: 8 trapezoidal and 2 square.
| Dual elongated square bipyramid | Net of dual |
|---|---|
 |
 |
Related polyhedra and Honeycombs
An elongated square bipyramid, similar to Johnson solid J15, allows a self-tessellation of Euclidean space. It can be considered a transitional phase between the cubic and rhombic dodecahedral honeycombs[1] The cells are here colored white, red, and blue based on their orientation in space. The square pyramid caps have shortened isosceles triangle faces, with six of these pyramids meeting together to form a cube.
[caution!]
Above honeycomb cannot be constructed by Elongated square bipyramid.
If this honeycomb exist, triangles are not regular(2:√3:√3).
Elongated square bipyramid (Johnson solid No.15) fill the space with Tetrahedron and either or combination of {Octahedron, Square pyramid(Johnson solid No.1)}.[3]
See also
References
- 1 2 Order in Space: A design source book, Keith Critchlow, p.46-47
- ↑ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ↑ http://woodenpolyhedra.web.fc2.com/J15.html
