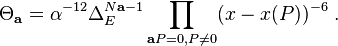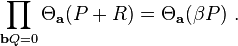Elliptic unit

In mathematics, elliptic units are certain units of abelian extensions of imaginary quadratic fields constructed using singular values of modular functions, or division values of elliptic functions. They were introduced by Gilles Robert in 1973, and were used by John Coates and Andrew Wiles in their work on the Birch and Swinnerton-Dyer conjecture. Elliptic units are an analogue for imaginary quadratic fields of cyclotomic units. They form an example of an Euler system.

A system of elliptic units may be constructed for an elliptic curve E with complex multiplication by the ring of integers R of an imaginary quadratic field F. For simplicity we assume that F has class number one. Let a be an ideal of R with generator α. For a Weierstrass model of E, define

\Theta_{\mathbf{a}} = \alpha^{-12} \Delta_E^{N\mathbf{a} - 1} \prod_{\mathbf{a}P=0, P\ne0} (x-x(P))^{-6} \ .

where Δ is the discriminant and x is the X-coordinate on the Weierstrass model. The function Θ is independent of the choice of model, and is defined over the field of definition of E.

Let b be an ideal of R coprime to a and Q an R-generator of the b-torsion. Then Θa(Q) is defined over the ray class field K(b), and if b is not a prime power then Θa(Q) is a global unit: if b is a power of a prime p then Θa(Q) is a unit away from p.

The function Θa satisfies a distribution relation for b = (β) coprime to a:

\prod_{\mathbf{b}Q=0} \Theta_{\mathbf{a}}(P+R) = \Theta_{\mathbf{a}}(\beta P) \ .

See also

References

This article is issued from Wikipedia - version of the Wednesday, March 11, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.