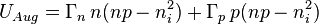Carrier generation and recombination

In the solid-state physics of semiconductors, carrier generation and recombination are processes by which mobile charge carriers (electrons and electron holes) are created and eliminated. Carrier generation and recombination processes are fundamental to the operation of many optoelectronic semiconductor devices, such as photodiodes, LEDs and laser diodes. They are also critical to a full analysis of p-n junction devices such as bipolar junction transistors and p-n junction diodes.

The electron–hole pair is the fundamental unit of generation and recombination, corresponding to an electron transitioning between the valence band and the conduction band.

Band structure

Like other solids, semiconductor materials have an electronic band structure determined by the crystal properties of the material. The actual energy distribution among the electrons is described by the Fermi level and the temperature of the electrons. At absolute zero temperature, all of the electrons have energy below the Fermi level; but at non-zero temperatures the energy levels are filled following a Boltzmann distribution.

Electronic band structure of a semiconductor material.

In semiconductors the Fermi level lies in the middle of a forbidden band or band gap between two allowed bands called the valence band and the conduction band. The valence band, immediately below the forbidden band, is normally very nearly completely occupied. The conduction band, above the Fermi level, is normally nearly completely empty. Because the valence band is so nearly full, its electrons are not mobile, and cannot flow as electric current.

However, if an electron in the valence band acquires enough energy to reach the conduction band, it can flow freely among the nearly empty conduction band energy states. Furthermore, it will also leave behind an electron hole that can flow as current exactly like a physical charged particle. Carrier generation describes processes by which electrons gain energy and move from the valence band to the conduction band, producing two mobile carriers; while recombination describes processes by which a conduction band electron loses energy and re-occupies the energy state of an electron hole in the valence band.

In a material at thermal equilibrium generation and recombination are balanced, so that the net charge carrier density remains constant. The equilibrium carrier density that results from the balance of these interactions is predicted by thermodynamics. The resulting probability of occupation of energy states in each energy band is given by Fermi–Dirac statistics.

Generation and recombination processes

Carrier generation and recombination occur when an electron makes transition from the valence band to conduction band in a semiconductor, as a result of interaction with other electrons, holes, photons, or the vibrating crystal lattice itself. These processes must conserve both quantized energy and momentum, and the vibrating lattice plays a large role in conserving momentum as photons carry very little momentum in relation to their energy.

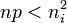Recombination and generation are always happening in semiconductors, both optically and thermally, and their rates are in balance at equilibrium. The product of the electron and hole densities ( $n$ and $p$ ) is a constant $(n_o p_o=n_i^2)$ at equilibrium, maintained by recombination and generation occurring at equal rates. When there is a surplus of carriers (i.e., $n p>n_i^2$ ), the rate of recombination becomes greater than the rate of generation, driving the system back towards equilibrium. Likewise, when there is a deficit of carriers (i.e., $n p<n_i^2$ ), the generation rate becomes greater than the recombination rate, again driving the system back towards equilibrium.^[1] As the electron moves from one energy band to another, the energy and momentum that it has lost or gained must go to or come from the other particles involved in the process (e.g. photons, electron, or the system of vibrating lattice atoms). The following models are used to describe generation and recombination, depending on which particles are involved in the process.

The following image shows change in excess carriers being generated (green:electrons and purple:holes) with increasing light intensity (Generation rate /cm3) at the center of an intrinsic semiconductor bar. Electrons have higher diffusion constant than holes leading to fewer excess electrons at the center as compared to holes.

Shockley–Read–Hall (SRH) process

In Shockley-Read-Hall recombination, also called trap-assisted recombination, the electron in transition between bands passes through a new energy state (localized state) created within the band gap by an impurity in the lattice; such energy states are called deep-level traps. The localized state can absorb differences in momentum between the carriers, and so this process is the dominant generation and recombination process in silicon and other indirect bandgap materials. It can also dominate in direct bandgap materials under conditions of very low carrier densities (very low level injection). The energy is exchanged in the form of lattice vibration, a phonon exchanging thermal energy with the material. The process is named after William Shockley, William Thornton Read^[2] and Robert N. Hall.^[3]

Radiative recombination

During radiative recombination, a form of spontaneous emission, a photon is emitted with the wavelength corresponding to the energy released. This effect is the basis of LEDs. Because the photon carries relatively little momentum, radiative recombination is significant only in direct bandgap materials.

When photons are present in the material, they can either be absorbed, generating a pair of free carriers, or they can stimulate a recombination event, resulting in a generated photon with similar properties to the one responsible for the event. Absorption is the active process in photodiodes, solar cells, and other semiconductor photodetectors, while stimulated emission is responsible for laser action in laser diodes.

Auger recombination

In Auger recombination the energy is given to a third carrier, which is excited to a higher energy level without moving to another energy band. After the interaction, the third carrier normally loses its excess energy to thermal vibrations. Since this process is a three-particle interaction, it is normally only significant in non-equilibrium conditions when the carrier density is very high. The Auger effect process is not easily produced, because the third particle would have to begin the process in the unstable high-energy state.

The Auger recombination can be calculated from the equation :

U_{Aug} = \Gamma_n \,n(np-n_i^2) + \Gamma_p \,p(np-n_i^2)

Auger recombination in LEDs

The mechanism causing LED efficiency droop was identified in 2007 as Auger recombination, which met with a mixed reaction.^[4] In 2013, an experimental study claimed to have identified Auger recombination as the cause of efficiency droop.^[5] However, it remains disputed whether the amount of Auger loss found in this study is sufficient to explain the droop. Other frequently quoted evidence against Auger as the main droop causing mechanism is the low-temperature dependence of this mechanism which is opposite to that found for the droop.

References

↑ A. Elhami Khorasani, D. K. Schroder, T. L. Alford, IEEE Trans. Electron Dev., vol. 35, pp. 986-988, 2014
↑ Shockley, W.; Read, W. T. (1 September 1952). "Statistics of the Recombinations of Holes and Electrons". Physical Review 87 (5): 835–842. doi:10.1103/PhysRev.87.835.
↑ Hall, R.N. (1951). "Germanium rectifier characteristics". Physical Review 83 (1): 228.
↑ Stevenson, Richard (August 2009) The LED’s Dark Secret: Solid-state lighting won't supplant the lightbulb until it can overcome the mysterious malady known as droop. IEEE Spectrum
↑ Justin Iveland, Lucio Martinelli, Jacques Peretti, James S. Speck, Claude Weisbuch. "Cause of LED Efficiency Droop Finally Revealed". Physical Review Letters, 2013. Science Daily. Retrieved 23 April 2013.

N.W. Ashcroft and N.D. Mermin, Solid State Physics, Brooks Cole, 1976

External links

This article is issued from Wikipedia - version of the Tuesday, January 05, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.