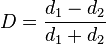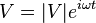Electrodynamic droplet deformation

Electrodynamic droplet deformation is a phenomenon that occurs when liquid droplets suspended in a second immiscible liquid are exposed to an oscillating electric field. Under these conditions, the droplet will periodically deform between prolate and oblate ellipsoidal shapes. The characteristic frequency and magnitude of the deformation is determined by a balance of electrodynamic, hydrodynamic, and capillary stresses acting on the droplet interface. This phenomenon has been studied extensively both mathematically and experimentally because of the complex fluid dynamics that occur. Characterization and modulation of electrodynamic droplet deformation is of particular interest for engineering applications because of the growing need to improve the performance of complex industrial processes(e.g. two-phase cooling,[1] crude oil demulsification). The primary advantage of using oscillatory droplet deformation to improve these engineering processes is that the phenomenon does not require sophisticated machinery or the introduction of heat sources. This effectively means that improving performance via oscillatory droplet deformation is simple and in no way diminishes the effectiveness of the existing engineering system.
Motivation
The heat transfer dynamics in two-phase two component flow systems are governed by the dynamic behavior of droplets/bubbles that are injected into the circulating coolant stream.[2][3] The injected bubbles/droplets are typically of a lower density than the coolant and thus experience an upward buoyancy force. They enhance the thermal performance of cooling systems because as they float upwards in heated pipes the coolant is forced to flow around the bubbles/droplets. The secondary flow around the droplets modifies the coolant flow creating a quasi-mixing effect in the bulk fluid that increases the heat transfer from the pipe walls to the coolant. Current two-component, two-phase cooling systems such as nuclear reactors, control the cooling rate by optimizing solely the coolant type, flow rate, and bubble/droplet injection rate. This approach modifies only bulk flow settings and does not provide engineers the option of control of directly modulating the mechanisms that govern the heat transfer dynamics. Inducing oscillations in the bubbles/droplets is a promising approach to improving convective cooling because creates secondary and tertiary flow patterns that could improve heat transfer without introducing significant heat to the system.
Electrodynamic droplet deformation also of particular interest in crude oil processing as a method to improve the separation rate of water and salts from the bulk. In its unprocessed form, crude oil cannot be used directly in industrial processes because the presence of salts can corrode heat exchangers and distillation equipment. To avoid fouling due to these impurities it is necessary to first remove the salt, which is concentrated in suspended water droplets. Exposing batches of crude oil to both DC and AC high-voltage electric fields induces droplet deformation that ultimately causes the water droplets to coalesce into larger droplets. Droplet coalescence improves the separation rate of water from crude oil because the upward velocity of a sphere is proportional to the square of the sphere’s radius. This can be easily shown by considering gravitational force, buoyancy, and Stokes flow drag. It has been reported that increasing both the amplitude and frequency of the applied electric fields can significantly increases water separation up to 90%.[4]
Taylor’s 1966 Solution
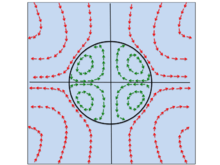
Taylor’s 1966 solution[5] to internal and external flow of a sphere induced by an electric field was the first to provide an argument that accounted for pressure induced by fluid flow both inside the droplet and in the external fluid field. Unlike some of his contemporaries, Taylor argued that surface tension and a uniform internal pressure could not balance the spatially varying normal stress on a droplet interface that was resulted from the presence of a steady, uniform electric field. He posited that in order for a droplet interface to remain in a non-deformed state in the presence of an electric field, there must be fluid flow both inside and outside the droplet interface. He developed a solution for the internal and external flow field using a streamfunction approach similar to that of creeping flow past a sphere.[6] Taylor confirmed the validity of his solution by comparing it to images from flow visualization studies that observed circulation both inside and outside the droplet interface.
Torza's Solution
Torza’s 1971 solution[7] for droplet deformation under the presence of a uniform, time-varying electric field is the most widely reference model for predicting small amplitude droplet deformations. Similar to the solution developed by Taylor, Torza developed a solution for electrodynamic droplet deformation by considering fluid circulation both inside and outside of a droplet interface. His solution is innovative because it derives an expression for the instantaneous droplet deformation ratio by considering separate sub-problems to derive the effects of electric stress, internal hydrodynamic stress, external hydrodynamic stress, and the surface tension on the droplet interface. The droplet deformation ratio D is a quantity that expresses the relative extension and shortening of the vertical and horizontal dimensions of a sphere.
The electric stress sub-problem is formulated by defining electric potential fields on the inside and outside of the droplet interface that are expressible as complex phasors with the oscillation frequency as the imposed electric field.
Since Torza treats the fluid inside the droplet and outside the droplet as having no net charge, the governing equation for the electric stress sub-problem reduces to Gauss Law with a spatial charge density of zero. By re-expressing the electric field in terms of the gradient of the electric potential, the governing electric equation reduces to the Laplace Equation. Separation of variables can be used to derive a solution to this equation of the form of a power series multiplied by the cosine of the polar angle taken relative to the direction of the electric field. Using the solutions for the magnitude of the electric potentials on the inside and outside of the droplet, the electric stress created on the bubble/droplet interface can be determined using the definition of the Maxwell Stress Tensor and neglecting the electric field.
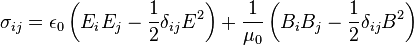
It is worth noting that because the electric field is in the form of a phasor, the scalar product and tensor product of electric field with itself, as are present in the Maxwell Stress Tensor, result in a doubling of the oscillation frequency. The sub-problem Torza solves to determine the velocity fields and hydrodynamic stresses that result from the electric stress is of exactly the same form as the one Taylor used for his solution for steady electric fields. Specifically, Torza solves the streamfunction formulation of the curl of the Navier-Stokes Equations in spherical coordinates by adopting Taylor’s streamfunction solution form and imposing stress balance conditions at the interface. Using the streamfunction solution, Torza derived analytical expressions for the velocity fields that could be used to derive analytical expressions for hydrodynamic stress on the interface for incompressible Newtonian fluids.
![0= \left[
\frac{\partial^2}{\partial r^2} +
\frac{\sin \theta}{r^2} \frac{\partial}{\partial \theta}\left(\frac{1}{\sin(\theta)^2} \frac{\partial }{\partial \theta}\right)
\right]^2 \psi.](../I/m/f74cf1552895ff60e28fffd1e4ef43cd.png)
![\psi = \left[\frac{C_1 b^4}{r^2} + C_2 b^2 + \frac{C_3}{b r^3} + \frac{C_4 r^5}{ b^3})\right] \sin(\theta)^2 \cos(\theta).](../I/m/23af4a75181e7533999bc31cedc98a1a.png)
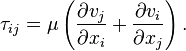
To incorporate the effect of surface tension into the periodic deformation of a droplet, Torza calculated the difference in electric and hydrodynamic stresses across the interface and used that as the driving stress in the Laplace Pressure Equation. This is the most important relation for this system because it describes the mechanism by which differences in stress across the droplet interface can induce deformation by inducing a change of the principle radii of curvature.
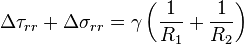
Using this relation between surface pressures in conjunction with geometrical arguments derived by Taylor for small deformations, Torza was able to derive an analytical expression for the deformation ratio as the sum of a steady component and an oscillating component with a frequency that is twice that of the imposed electric field as shown.
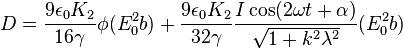
The important terms to recognize in this expression are  in the steady term, the cosine in the time-varying term, and gamma in both terms. The phi term is what Taylor and Torza refer to as a “discriminating function” because its value determines whether the droplet will tend to spend more time in either a prolate or oblate shape. It is a function of all the material properties and the frequency of oscillation, but is completely independent of time. The time varying cosine term shows that the droplet does in fact oscillate at twice the frequency of the imposed electric field but is also generally out of phase due to the constant alpha term that arises due to the mathematics. The other variables are constants that depend on the geometric, electric, and thermodynamic properties of the relevant liquids in addition to the oscillation frequency.
in the steady term, the cosine in the time-varying term, and gamma in both terms. The phi term is what Taylor and Torza refer to as a “discriminating function” because its value determines whether the droplet will tend to spend more time in either a prolate or oblate shape. It is a function of all the material properties and the frequency of oscillation, but is completely independent of time. The time varying cosine term shows that the droplet does in fact oscillate at twice the frequency of the imposed electric field but is also generally out of phase due to the constant alpha term that arises due to the mathematics. The other variables are constants that depend on the geometric, electric, and thermodynamic properties of the relevant liquids in addition to the oscillation frequency.
In general, it is apparent that the magnitude of the droplet deformation is constrained by the interfacial tension, represented by gamma. As the interfacial tension increases, the net magnitude decreases due to an increase in capillary forces. Since the equilibrium shape of a droplet tends towards the one with the minimum energy, a large value of interfacial tension tends to drive the droplet shape towards a sphere.
Safety and practical considerations
Although periodic droplet deformation is widely studied for its practical industrial applications, its implementation poses significant safety issues and physical limitations due to the use of electric field. In order to induce periodic droplet deformation using an electric field, an extremely large amplitude electric field must be applied. Research studies using water droplets suspended in silicon oil required root-mean-square values as high as 10^6 V/m . Even for a small electrode spacing, this type of field requires electric potentials greater than 500V, which is roughly three times wall voltage in the United States. Practically speaking, this large of an electric field can only be achieved if the electrode spacing is very small (~ O(0.1 mm)) or if a high-voltage amplifier is available. It is for this reason that the majority of studies of this phenomenon are currently being conducted in research laboratories using small diameter tubes; tubes of this size are in fact present in industrial cooling systems, such as nuclear reactors.
References
- ↑ Kaji NN, Mori YH, Tochitani YY. Electrically Induced Shape Oscillation of Drops as a Means of Direct-Contact Heat Transfer Enhancement: Part 2—Heat Transfer. J. Heat Transfer. 1988;110(3):700-704.
- ↑ S. Mostafa Ghiaasiaan. Two-Phase Flow, Boiling, and Condensation: In Conventional and Miniature Systems. 2008. Cambridge University Press
- ↑ Takaaki Mochizuki. Periodic Deformation of Microsize Droplets in a Microchannel Induced by a Transverse Alternating Electric Field. Langmuir 2013 29 (41)
- ↑ Byoung-Yun Kim, Jun Hyuk Moon, Tae-Hyun Sung, Seung-Man Yang, Jong-Duk Kim. Demulsification of water-in-crude oil emulsions by a continuous electrostatic dehydrator. Separation Science and Technology. Vol. 37, Iss. 6, 2002
- ↑ G. Taylor. (1966). Studies in Electrohydrodynamics. I. The Circulation Produced in a Drop by Electrical Field. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences.
- ↑ Pijush K. Kundu, Ira M. Cohen. Fluid Mechanics. 2010. Academic Press
- ↑ S. Torza, R. G. Cox, and S. G. Mason Electrohydrodynamic Deformation and Burst of Liquid Drops Phil. Trans. R. Soc. Lond. A February 18, 1971 269 1198 295-319