Electro-gyration
The electrogyration effect is the spatial dispersion phenomenon, that consists in the change of optical activity (gyration) of crystals by a constant or time-varying electric field. Being a spatial dispersion effect, the induced optical activity exhibit different behavior under the operation of wave vector reversal, when compared with the Faraday effect: the optical activity increment associated with the electrogyration effect changes its sign under that operation, contrary to the Faraday effect. Formally, it is a special case of gyroelectromagnetism obtained when the magnetic permeability tensor is diagonal.[1]
The electrogyration effect linear in the electric field occurs in crystals of all point groups of symmetry except for the three cubic – m3m, 432 and  . The effect proportional to the square of the electric field can exist only in crystals belonging to acentric point groups of symmetry.
. The effect proportional to the square of the electric field can exist only in crystals belonging to acentric point groups of symmetry.
The historical background of discovery of electrogyration
The changes in the optical activity sign induced by the external electric field have been observed for the first time in ferroelectric crystals LiH3(SeO4)2 by H. Futama and R. Pepinsky in 1961
,[2] while switching enantiomorphous ferroelectric domains (the change in the point symmetry group of the crystal being 2/m«m). The observed phenomenon has been explained as a consequence of specific domain structure (a replacement of optic axes occurred under the switching), rather than the electrogyration induced by spontaneous polarization.
The first description of electrogyration effect induced by the biasing field and spontaneous polarization at ferroelectric phase transitions has been proposed by K. Aizu in 1963 on the basis of third-rank axial tensors [3] (the manuscript received on September 9, 1963). Probably, K. Aizu has been the first who defined the electro-gyration effect (”the rate of change of the gyration with the biasing electric field at zero value of the biasing electric field is provisionally referred to as “electrogyration””) and introduced the term “electrogyration” itself.
Almost simultaneously with K. Aizu, I.S. Zheludev has suggested tensor description of the electrogyration in 1964 [4] (the manuscript received on February 21, 1964). In this paper the electrogyration has been referred to as “electro-optic activity”.
In 1969, O.G. Vlokh has measured for the first time the electrogyration effect induced by external biasing field in the quartz crystal and determined the coefficient of quadratic electro-gyration effect [5] (the manuscript received on July 7, 1969).
Thus, the electrogyration effect has been predicted simultaneously by Aizu K. and Zheludev I.S. in 1963–1964 and revealed experimentally in quartz crystals by Vlokh O.G. in 1969.[5]
.[6][7][8]
Later in 2003, the gyroelectricity has been extended to gyroelectromagnetic media,[1] which account for ferromagnetic semiconductors and engineered metamaterials, for which gyroelectricity and gyromagnetism (Faraday effect) may occur at the same time.
Description
Electrodynamics relations
The electric field and the electric displacement vectors of electromagnetic wave propagating in gyrotropic crystals may be written respectively as:
, (1)
or
, (2)
where 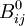 is the optical frequency impermeability tensor,
is the optical frequency impermeability tensor, 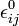 the dielectric permittivity tensor,
the dielectric permittivity tensor, 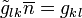 ,
,  the mean refractive index,
the mean refractive index,  - induction,
- induction,  ,
,  polar third rank tensors,
polar third rank tensors,  the unit antisymmetric Levi-Civit pseudo-tensor,
the unit antisymmetric Levi-Civit pseudo-tensor,  the wave vector, and
the wave vector, and 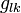 ,
, 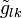 the second rank gyration pseudo-tensors. The specific rotation angle of the polarization plane
the second rank gyration pseudo-tensors. The specific rotation angle of the polarization plane  caused by the natural optical activity is defined by the relation:
caused by the natural optical activity is defined by the relation:
, (3)
where  is the refractive index,
is the refractive index, 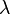 the wavelength,
the wavelength, 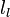 ,
,  the transformation coefficients between the Cartesian and spherical coordinate systems (
the transformation coefficients between the Cartesian and spherical coordinate systems (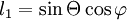 ,
, 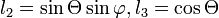 ), and
), and 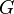 the pseudo-scalar gyration parameter.
The electro-gyration increment of gyration tensor occurred under the action of electric field
the pseudo-scalar gyration parameter.
The electro-gyration increment of gyration tensor occurred under the action of electric field  or/and
or/and 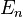 is written as:
is written as:
, (4)
where 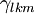 and
and  are third- and fourth-rank axial tensors describing the linear and quadratic electrogyration, respectively. In the absence of linear birefringence, electrogyration increment of the specific rotatory power is given by:
are third- and fourth-rank axial tensors describing the linear and quadratic electrogyration, respectively. In the absence of linear birefringence, electrogyration increment of the specific rotatory power is given by:
. (5)
The electrogyration effect may be also induced by spontaneous polarization 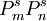 appearing in the course of ferroelectric phase transitions
appearing in the course of ferroelectric phase transitions
. (6)
Explanation on the basis of symmetry approach
The electrogyration effect can be easy explained on the basis of Curie and Neumann symmetry principles. In the crystals that exhibit centre of symmetry, natural gyration can not exist, since, due to the Neumann principle, the point symmetry group of the medium should be a subgroup of the symmetry group that describes the phenomena, which are properties of this medium. As a result, the gyration tensor possessing a symmetry of second-rank axial tensor - 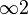 is not a subgroup of centrosymmetric media and so the natural optical activity cannot exist in such media. According to the Curie symmetry principle, external actions reduce the symmetry group of the medium down to the group defined by intersection of the symmetry groups of the action and the medium. When the electric field (with the symmetry of polar vector,
is not a subgroup of centrosymmetric media and so the natural optical activity cannot exist in such media. According to the Curie symmetry principle, external actions reduce the symmetry group of the medium down to the group defined by intersection of the symmetry groups of the action and the medium. When the electric field (with the symmetry of polar vector, 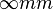 ) influences the crystal which possess the inversion centre, the symmetry group of the crystal should be lowered to the acentric one, thus permitting the appearance of gyration. However, in case of the quadratic electrogyration effect, the symmetry of the action should be considered as that of the dyad product
) influences the crystal which possess the inversion centre, the symmetry group of the crystal should be lowered to the acentric one, thus permitting the appearance of gyration. However, in case of the quadratic electrogyration effect, the symmetry of the action should be considered as that of the dyad product 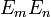 or, what is the same, the symmetry of a polar second-rank tensor (
or, what is the same, the symmetry of a polar second-rank tensor (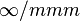 ). Such a centrosymmetric action cannot lead to lowering of centrosymmetric symmetry of crystal to acentric states. This is the reason why the quadratic electrogyration exists only in the acentric crystals.
). Such a centrosymmetric action cannot lead to lowering of centrosymmetric symmetry of crystal to acentric states. This is the reason why the quadratic electrogyration exists only in the acentric crystals.
Eigenwaves in the presence of electrogyration
In a general case of light propagation along optically anisotropic directions, the eigenwaves become elliptically polarized in the presence of electrogyration effect, including rotation of the azimuth of polarization ellipse. Then the corresponding ellipticity 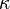 and the azimuth
and the azimuth 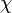 are defined respectively by the relations
are defined respectively by the relations
, (7)
, (8)
where 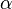 is the polarization azimuth of the incident light with respect to the principal indicatrix axis,
is the polarization azimuth of the incident light with respect to the principal indicatrix axis, 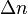 the linear birefringence,
the linear birefringence, 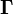 the phase retardation,
the phase retardation, 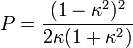 , and
, and 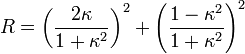 . In the case of light propagation along optically isotropic directions (i.e., the optic axes), the eigenwave become circularly polarized (
. In the case of light propagation along optically isotropic directions (i.e., the optic axes), the eigenwave become circularly polarized (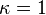 ), with different phase velocities and different signs of circular polarization (left and right ones). Hence the relation (8) may be simplified so as to describe a pure polarization plane rotation:
), with different phase velocities and different signs of circular polarization (left and right ones). Hence the relation (8) may be simplified so as to describe a pure polarization plane rotation:
, (9)
or
, (10)
where 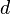 - is the sample thickness along the direction of light propagation.
For the directions of light propagation far from the optic axis, the ellipticity
- is the sample thickness along the direction of light propagation.
For the directions of light propagation far from the optic axis, the ellipticity 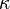 is small and so one can neglect the terms proportional to
is small and so one can neglect the terms proportional to 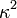 in Eq.(8). Thus, in order to describe the polarization azimuth at
in Eq.(8). Thus, in order to describe the polarization azimuth at  and the gyration tensor, simplified relations
and the gyration tensor, simplified relations
, (11)
or
. (12)
are often used.
According to Eq.(11), when the light propagates along anisotropic directions, the gyration (or the electro-gyration) effects manifest themselves as oscillations of the azimuth of polarization ellipse occurring with changing phase retardation 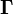 .
.
Experimental results
The electrogyration effect has been revealed for the first time in quartz crystals [2] as an effect quadratic in the external field. Later on, both the linear and quadratic
[10] electrogyrations has been studied in the dielectric (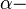 HIO3
,[11] LiIO3
,[12] PbMoO4,[13] NaBi(MoO4)2, Pb5SiO4(VO4)2, Pb5SeO4(VO4)2, Pb5GeO4(VO4)2,[14] alums [15][16]
[17] etc.) semiconductor (AgGaS2, CdGa2S4)
,[18] ferroelectric (TGS, Rochelle Salt, Pb5Ge3O11 and KDP families etc.)
[19]
[20]
[21]
,[22] as well as the photorefractive (Bi12SiO20, Bi12GeO20, Bi12TiO20) materials
[23]
[24]
.[25] The electro-gyration effect induced by a powerful laser radiation (a so-called self-induced or dynamic electro-gyration) has been studied in the works
[26]
.[27] The influence of electro-gyration on the photorefraction storage has been investigated in
,[28][29] too. From the viewpoint of nonlinear electrodynamics, the existence of gradient of the electric field of optical wave in the range of the unit cell corresponds to macroscopic gradient of the external electrical field, if only the frequency transposition [30] is taken into account. In that sense, the electrogyration effect represents the first of the gradient nonlinear optical phenomena ever revealed.
HIO3
,[11] LiIO3
,[12] PbMoO4,[13] NaBi(MoO4)2, Pb5SiO4(VO4)2, Pb5SeO4(VO4)2, Pb5GeO4(VO4)2,[14] alums [15][16]
[17] etc.) semiconductor (AgGaS2, CdGa2S4)
,[18] ferroelectric (TGS, Rochelle Salt, Pb5Ge3O11 and KDP families etc.)
[19]
[20]
[21]
,[22] as well as the photorefractive (Bi12SiO20, Bi12GeO20, Bi12TiO20) materials
[23]
[24]
.[25] The electro-gyration effect induced by a powerful laser radiation (a so-called self-induced or dynamic electro-gyration) has been studied in the works
[26]
.[27] The influence of electro-gyration on the photorefraction storage has been investigated in
,[28][29] too. From the viewpoint of nonlinear electrodynamics, the existence of gradient of the electric field of optical wave in the range of the unit cell corresponds to macroscopic gradient of the external electrical field, if only the frequency transposition [30] is taken into account. In that sense, the electrogyration effect represents the first of the gradient nonlinear optical phenomena ever revealed.
See also
- Piezo-gyration
- Faraday effect
References
- 1 2 Prati E. (2003) "Propagation in gyroelectromagnetic guiding systems", J. of Electr. Wav. and Appl. 17, 8, 1177
- ↑ Futama H. and Pepinsky R. (1962) "Optical activity in ferroelectric LiH3(SeO3)2", J. Phys. Soc. Jap. 17, 725
- ↑ Aizu K. (1964) “Reversal in optical rotatory power – “gyroelectric” crystals and “hypergyroelectric” crystals”, Phys. Rev. 133 (6A) A1584–A1588
- ↑ Zheludev I.S. (1964), "Axial tensors of the third rank and the physical effects they describe", Kristallografiya 9, 501-505.[(1965). Sov.Phys.Crystallogr. 9,418]
- 1 2 Vlokh O.G.(1970). "Electrooptical activity of quartz crystals", Ukr.Fiz.Zhurn.15(5), 758-762.[Blokh O.G. (1970). "Electrooptical activity of quartz crystals", Sov.Phys. Ukr.Fiz.Zhurn.15, 771.]
- ↑ Vlokh O.G. (1971) "Electrogyration effects in quartz crystals", Pis.ZhETF. 13, 118-121 [Blokh O.G. (1971) "Electrogyration effects in quartz crystals", Sov.Phys. Pis.ZhETF. 13, 81-83.]
- ↑ Vlokh O.G. (1987), "Electrogyration properties of crystals" Ferroelectrics 75, 119-137.
- ↑ Vlokh O.G. (2001) "The historical background of the finding of electrogyration", Ukr.J.Phys.Opt., 2(2), 53-57
- ↑ Vlokh O.G., Kutniy I.V., Lazko L.A., and Nesterenko V.Ya. (1971) "Electrogyration of crystals and phase transitions", Izv.AN SSSR, ser.fiz. XXXV (9), 1852-1855.
- ↑ Vlokh O.G., Krushel'nitskaya T.D. (1970). "Axial four-rank tensors and quadratic electrogyration", Kristallografiya 15(3), 587-589 [Vlokh O.G., Krushel'nitskaya T.D. (1970). "Axial four-rank tensors and quadratic electrogyration", Sov.Phys.Crystallogr., 15(3)]
- ↑ Vlokh O.G., Lazko L.A.and Nesterenko V.Ya. (1972). "Revealing of the linear electrogyration effect in
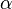 HIO3 crystals", Kristallografiya, 17(6), 1248-1250.[Sov.Phys.Crystallogr.,17(6)]
HIO3 crystals", Kristallografiya, 17(6), 1248-1250.[Sov.Phys.Crystallogr.,17(6)] - ↑ Vlokh O.G., Laz'ko L.A., Zheludev I.S. (1975). "Effect of external factors on gyrotropic properties of LiIO3 crystals", Kristallografiya 20(3), 654-656 [Sov.Phys.Crystallogr.,20(3), 401]
- ↑ Vlokh, O. G.; Zheludev, I. S.; Klimov, I. M. (1975). "Electric field-induced optical activity of centrosymmetrical crystals of lead molybdate PbMoO4 /Electrogyration/" [Optical activity of the centrosymmetric crystals of lead molibdate - PbMoO4, induced by electric field (electrogyration)] (PDF). Doklady Akademii Nauk SSSR 223 (6): 1391–1393. Bibcode:1975DoSSR.223.1391V.
- ↑ Vlokh O.G. (1984) Spatial dispersion phenomena in parametric crystal optics. Lviv: Vyshcha Shkola (in Russian).
- ↑ Weber H.J. and Haussuhl S. (1974), "Electric-Field-Induced Optical Activity and Circular Dichroism of Cr-Doped KAl(SO4)2 · 12H2O " Phys. Stat. Sol.(b) 65, 633-639.
- ↑ Weber H.J. and Haussuhl S. (1979), "Electrogyration and piezogyration in NaClO3" Acta Crystallogr. A35225-232.
- ↑ Weber H.J., Haussuhl S. (1976) "Electrogyration effect in alums", Acta Crystallogr. A32 892-895
- ↑ Vlokh O.G., Zarik A.V., Nekrasova I.M. (1983), "On the electrogyration in AgGaS2 and CdGa2S4 crystals", Ukr.Fiz.Zhurn., 28(9), 1334-1338.
- ↑ Kobayashi J., Takahashi T., Hosakawa T. and Uesu Y. (1978). "A new method for measuring the optical activity of crystals and the optical activity of KH2PO4 ", J.Appl. Phys. 49, 809-815.
- ↑ Kobayashi J., Uesu Y. and Sorimachi H. (1978), "Optical activity of some non-enantiomorphous ferroelectrics", Ferroelectrics. 21, 345-346.
- ↑ Uesu Y., Sorimachi H. and Kobayashi J. (1979), "Electrogyration of a Nonenantiomorphic Crystal, Ferroelectric KH2PO4 " Phys. Rev. Lett. 42, 1427-1430.
- ↑ Vlokh O.G., Lazgko L.A., Shopa Y.I. (1981), "Electrooptic and Electrogyration Properties of the Solid Solutions on the Basis of Lead Germanate", Phys.Stat.Sol. (a) 65: 371-378.
- ↑ Vlokh O.G., Zarik A.V. (1977), "The effect of electric field on the polarization of light in the Bi12SiO20, Bi12GeO20, NaBrO3 crystals", Ukr.Fiz.Zhurn. 22(6), 1027-1031.
- ↑ Deliolanis N.C., Kourmoulis I.M., Asimellis G., Apostolidis A.G., Vanidhis E.D., and Vainos N.A. (2005), "Direct measurement of the dispersion of electrogyration coefficient of photorefractive Bi12GeO20", J. Appl. Phys. 97, 023531.
- ↑ Deliolanis N.C, Vanidhis E.D, and Vainos N.A. (2006), "Dispersion of electogyration in sillenite crystals", Appl. Phys. B 85(4), 591-596.
- ↑ Akhmanov S.A., Zhdanov B.V., Zheludev N.I., Kovrigin N.I., Kuznetsov V.I. (1979). "Nonlinear optical activity in crystals", Pis.ZhETF. 29, 294-298.
- ↑ Zheludev N.I., Karasev V.Yu., Kostov Z.M. Nunuparov M.S.(1986) "Giant exciton resonance in nonlinear optical activity", Pis.ZhETF, 43(12), 578-581.
- ↑ Brodin M.S., Volkov V.I., Kukhtarev N.V. and Privalko A.V. (1990), "Nanosecond electrogyration selfdiffraction in Bi12TiO20 (BTO) crystal", Optics Communications, 76(1), 21-24.
- ↑ Kukhtarev N.V., Dovgalenko G.E. (1986) "Self-diffraction electrogyration and electroellipticity in centrosymmetric crystals", Sov.J. Quantum Electron., , 16 (1), 113-114.
- ↑ Vlokh R.O. (1991). "Nonlinear medium polarization with account of gradient invariants.", Phys. Stat.Sol (b), 168, k47-K50.