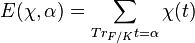Eisenstein sum

Not to be confused with Eisenstein series.

In mathematics, an Eisenstein sum is a finite sum depending on a finite field and related to a Gauss sum. Eisenstein sums were introduced by Gotthold Eisenstein (1848), named "Eisenstein sums" by Stickelberger (1890), and rediscovered by Yamamoto (1985), who called them relative Gauss sums.

Definition

The Eisenstein sum is given by

E(\chi,\alpha)=\sum_{Tr_{F/K}t=\alpha}\chi(t)

where F is a finite extension of the finite field K, and χ is a character of the multiplicative group of F, and α is an element of K (Lemmermeyer 2000, p. 133).

References

Berndt, Bruce C.; Evans, Ronald J. (1979), "Sums of Gauss, Eisenstein, Jacobi, Jacobsthal, and Brewer", Illinois Journal of Mathematics 23 (3): 374–437, ISSN 0019-2082, MR 537798, Zbl 0393.12029
Eisenstein, Gotthold (1848), "Zur Theorie der quadratischen Zerfällung der Primzahlen 8n + 3,7n + 2 und 7n + 4", Journal für Reine und Angewandte Mathematik 37: 97–126, ISSN 0075-4102
Lemmermeyer, Franz (2000), Reciprocity laws, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-66957-9, MR 1761696, Zbl 0949.11002
Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Encyclopedia of Mathematics and Its Applications 20 (2nd ed.), Cambridge University Press, ISBN 0-521-39231-4, Zbl 0866.11069
Yamamoto, K. (1985), "On congruences arising from relative Gauss sums", Number theory and combinatorics. Japan 1984 (Tokyo, Okayama and Kyoto, 1984), Singapore: World Sci. Publishing, pp. 423–446, MR 827799, Zbl 0634.12017

This article is issued from Wikipedia - version of the Sunday, July 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.