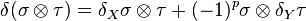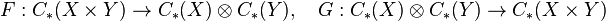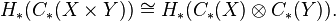Eilenberg–Zilber theorem
In mathematics, specifically in algebraic topology, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space 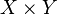 and those of the spaces
and those of the spaces  and
and 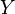 . The theorem first appeared in a 1953 paper in the American Journal of Mathematics.
. The theorem first appeared in a 1953 paper in the American Journal of Mathematics.
Statement of the theorem
The theorem can be formulated as follows. Suppose  and
and 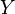 are topological spaces, Then we have the three chain complexes
are topological spaces, Then we have the three chain complexes 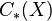 ,
, 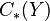 , and
, and 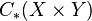 . (The argument applies equally to the simplicial or singular chain complexes.) We also have the tensor product complex
. (The argument applies equally to the simplicial or singular chain complexes.) We also have the tensor product complex 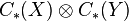 , whose differential is, by definition,
, whose differential is, by definition,
for 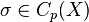 and
and 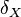 ,
, 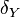 the differentials on
the differentials on 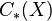 ,
,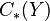 .
.
Then the theorem says that we have chain maps
such that 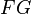 is the identity and
is the identity and 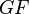 is chain-homotopic to the identity. Moreover, the maps are natural in
is chain-homotopic to the identity. Moreover, the maps are natural in  and
and 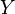 . Consequently the two complexes must have the same homology:
. Consequently the two complexes must have the same homology:
An important generalisation to the non-abelian case using crossed complexes is given in the paper by Tonks below. This give full details of a result on the (simplicial) classifying space of a crossed complex stated but not proved in the paper by Brown and Higgins on classifying spaces.
Consequences
The Eilenberg–Zilber theorem is a key ingredient in establishing the Künneth theorem, which expresses the homology groups 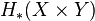 in terms of
in terms of 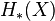 and
and 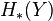 . In light of the Eilenberg–Zilber theorem, the content of the Künneth theorem consists in analysing how the homology of the tensor product complex relates to the homologies of the factors.
. In light of the Eilenberg–Zilber theorem, the content of the Künneth theorem consists in analysing how the homology of the tensor product complex relates to the homologies of the factors.
References
- Eilenberg, Samuel; Zilber, J. A. (1953), "On Products of Complexes", Amer. Jour. Math. (American Journal of Mathematics, Vol. 75, No. 1) 75 (1), pp. 200–204, doi:10.2307/2372629, JSTOR 2372629, MR 52767.
- Hatcher, Allen (2002), Algebraic Topology, Cambridge University Press, ISBN 0-521-79540-0.
- Tonks, Andrew (2003), "On the Eilenberg-Zilber theorem for crossed complexes", Jour. Pure Applied Algebra 179, pp. 199–230.
- Brown, Ronald; Higgins, Philip J. (1991), "The classifying space of a crossed complex", Proc. Camb. Phil. Soc. 110, pp. 95–120, doi:10.1017/S0305004100070158.