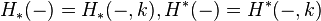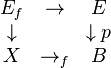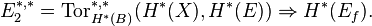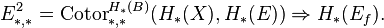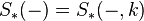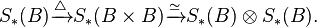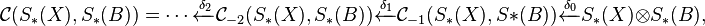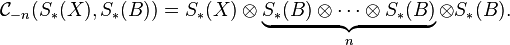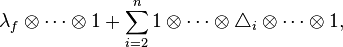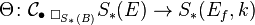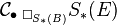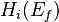Eilenberg–Moore spectral sequence

In mathematics, in the field of algebraic topology, the Eilenberg–Moore spectral sequence addresses the calculation of the homology groups of a pullback over a fibration. The spectral sequence formulates the calculation from knowledge of the homology of the remaining spaces. Samuel Eilenberg and John C. Moore's original paper addresses this for singular homology.

Motivation

Let $k$ be a field and

H_\ast(-)=H_\ast(-,k), H^\ast(-)=H^\ast(-,k)

denote singular homology and singular cohomology with coefficients in k, respectively.

Consider the following pullback E_f of a continuous map p:

\begin{array}{c c c} E_f &\rightarrow & E \\ \downarrow & & \downarrow{p}\\ X &\rightarrow_{ f} &B\\ \end{array}

A frequent question is how the homology of the fiber product E_f, relates to the ones of B, X and E. For example, if B is a point, then the pullback is just the usual product E × X. In this case the Künneth formula says

H^∗(E_f) = H^∗(X×E) ≅ H^∗(X) ⊗_k H^∗(E).

However this relation is not true in more general situations. The Eilenberg−Moore spectral sequence is a device which allows the computation of the (co)homology of the fiber product in certain situations.

Statement

The Eilenberg−Moore spectral sequences generalizes the above isomorphism to the situation where p is a fibration of topological spaces and the base B is simply connected. Then there is a convergent spectral sequence with

E_2^{\ast,\ast}=\text{Tor}_{H^\ast(B)}^{\ast,\ast}(H^\ast(X),H^\ast(E))\Rightarrow H^\ast(E_f).

This is a generalization insofar as the zeroeth Tor functor is just the tensor product and in the above special case the cohomology of the point B is just the coefficient field k (in degree 0).

Dually, we have the following homology spectral sequence:

E^2_{\ast,\ast}=\text{Cotor}^{H_\ast(B)}_{\ast,\ast}(H_\ast(X),H_\ast(E))\Rightarrow H_\ast(E_f).

Indications on the proof

The spectral sequence arises from the study of differential graded objects (chain complexes), not spaces. The following discusses the original homological construction of Eilenberg and Moore. The cohomology case is obtained in a similar manner.

Let

S_\ast(-)=S_\ast(-,k)

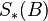be the singular chain functor with coefficients in $k$ . By the Eilenberg–Zilber theorem, $S_\ast(B)$ has a differential graded coalgebra structure over $k$ with structure maps

S_\ast(B)\xrightarrow{\triangle} S_\ast(B\times B)\xrightarrow{\simeq}S_\ast(B)\otimes S_\ast(B).

In down-to-earth terms, the map assigns to a singular chain s: Δⁿ → B the composition of s and the diagonal inclusion B ⊂ B × B. Similarly, the maps $f$ and $p$ induce maps of differential graded coalgebras

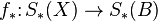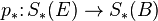$f_\ast \colon S_\ast(X)\rightarrow S_\ast(B)$ , $p_\ast \colon S_\ast(E)\rightarrow S_\ast(B)$ .

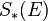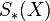In the language of comodules, they endow $S_\ast(E)$ and $S_\ast(X)$ with differential graded comodule structures over 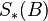$S_\ast(B)$ , with structure maps

S_\ast(X)\xrightarrow{\triangle} S_\ast(X)\otimes S_\ast(X)\xrightarrow{f_\ast\otimes 1} S_\ast(B)\otimes S_\ast(X)

and similarly for E instead of X. It is now possible to construct the so-called cobar resolution for

S_\ast(X)

as a differential graded 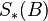$S_\ast(B)$ comodule. The cobar resolution is a standard technique in differential homological algebra:

\mathcal{C}(S_\ast(X),S_\ast(B))=\cdots\xleftarrow{\delta_2} \mathcal{C}_{-2}(S_\ast(X),S_\ast(B))\xleftarrow{\delta_1} \mathcal{C}_{-1}(S_\ast(X),S \ast(B))\xleftarrow{\delta_0} S_\ast(X)\otimes S_\ast(B),

where the n-th term $\mathcal{C}_{-n}$ is given by

\mathcal{C}_{-n}(S_\ast(X),S_\ast(B))=S_\ast(X)\otimes \underbrace{S_\ast(B)\otimes \cdots \otimes S_\ast(B)}_{n}\otimes S_\ast(B).

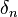The maps $\delta_n$ are given by

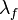\lambda_f\otimes\cdots\otimes 1 + \sum_{i=2}^n 1\otimes\cdots \otimes\triangle_i\otimes\cdots\otimes 1,

where $\lambda_f$ is the structure map for 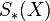$S_\ast(X)$ as a left 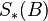$S_\ast(B)$ comodule.

The cobar resolution is a bicomplex, one degree coming from the grading of the chain complexes S_∗(−), the other one is the simplicial degree n. The total complex of the bicomplex is denoted 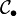$\mathbf{\mathcal{C}}_\bullet$ .

The link of the above algebraic construction with the topological situation is as follows. Under the above assumptions, there is a map

\Theta\colon \mathbf{\mathcal{C}}_{\bullet {\text{ }\Box_{S_\ast(B)}}}S_\ast(E)\rightarrow S_\ast(E_f,k)

that induces a quasi-isomorphism (i.e. inducing an isomorphism on homology groups)

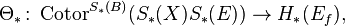
\Theta_\ast \colon \operatorname{Cotor}^{S_\ast(B)}(S_\ast(X)S_\ast(E))\rightarrow H_\ast(E_f),

where 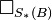$\Box_{S_\ast(B)}$ is the cotensor product and Cotor (cotorsion) is the derived functor for the cotensor product.

To calculate

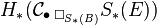H_\ast(\mathbf{\mathcal{C}}_{\bullet {\text{ }\Box_{S_\ast(B)}}}S_\ast(E))

view

\mathbf{\mathcal{C}}_{\bullet {\text{ }\Box_{S_\ast(B)}}}S_\ast(E)

as a double complex.

For any bicomplex there are two filtrations (see (McCleary 2001) or the spectral sequence of a filtered complex); in this case the Eilenberg−Moore spectral sequence results from filtering by increasing homological degree (by columns in the standard picture of a spectral sequence). This filtration yields

E^2=\operatorname{Cotor}^{H_\ast(B)}(H_\ast(X),H_\ast(E)).

These results have been refined in various ways. For example (Dwyer 1975) refined the convergence results to include spaces for which

\pi_1(B)

acts nilpotently on

H_i(E_f)

for all $i\geq 0$ and (Shipley 1996) further generalized this to include arbitrary pullbacks.

The original construction does not lend itself to computations with other homology theories since there is no reason to expect that such a process would work for a homology theory not derived from chain complexes. However, it is possible to axiomatize the above procedure and give conditions under which the above spectral sequence holds for a general (co)homology theory, see Smith's original work (Smith 1970) or the introduction in (Hatcher 2002).

References

Dwyer, William G. (1975), "Exotic convergence of the Eilenberg–Moore spectral sequence", Illinois Journal of Mathematics 19 (4): 607–617, ISSN 0019-2082
Eilenberg, Samuel; Moore, John C. (1962), "Limits and spectral sequences", Topology. An International Journal of Mathematics 1 (1): 1–23, doi:10.1016/0040-9383(62)90093-9
Hatcher, Allen (2002), Algebraic topology, Cambridge University Press, ISBN 978-0-521-79540-1
McCleary, John (2001), "Chapters 7 and 8: The Eilenberg−Moore spectral sequence I and II", A user's guide to spectral sequences, Cambridge Studies in Advanced Mathematics 58, Cambridge University Press, ISBN 978-0-521-56759-6
Shipley, Brooke E. (1996), "Convergence of the homology spectral sequence of a cosimplicial space", American Journal of Mathematics 118 (1): 179–207, doi:10.1353/ajm.1996.0004
Smith, Larry (1970), Lectures on the Eilenberg−Moore spectral sequence, Lecture Notes in Mathematics 134, Berlin, New York: Springer-Verlag, MR 0275435

Eilenberg–Moore spectral sequence

Motivation

Statement

Indications on the proof

References

Further reading