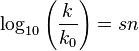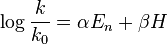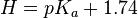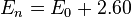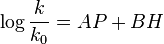Edwards equation

The Edwards equation in organic chemistry is a two-parameter equation for correlating nucleophilic reactivity, as defined by relative rate constants, with the basicity of the nucleophile (relative to protons) and its polarizability. This equation was first developed by John O. Edwards in 1954[1] and later revised based on additional work in 1956. [2] The general idea is that most nucleophiles are also good bases because the concentration of negatively charged electron density that defines a nucleophile will strongly attract positively charged protons, which is the definition of a base according to Brønsted-Lowry acid-base theory. Additionally, highly polarizable nucleophiles will have greater nucleophilic character than suggested by their basicity because their electron density can be shifted with relative ease to concentrate in one area.

History

Prior to Edwards developing his equation, other scientists were also working to define nucleophilicity quantitatively. Brønsted and Pederson first discovered the relationship between basicity, with respect to protons, and nucleophilicity in 1924:[3]

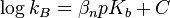
where \log k _B = \beta_n pK_{b} + C

where kb is the rate constant for nitramide decomposition by a base (B) and βN is a parameter of the equation.

Swain and Scott later tried to define a more specific and quantitative relationship by correlating nucleophilic data with a single-parameter equation[4][5] derived in 1953:

\log_{10}\left(\frac{k}{k_0}\right) = sn

This equation relates the rate constant k, of a reaction, normalized to that of a standard reaction with water as the nucleophile (k0), to a nucleophilic constant n for a given nucleophile and a substrate constant s that depends on the sensitivity of a substrate to nucleophilic attack (defined as 1 for methyl bromide). This equation was modeled after the Hammett equation.

However, both the Swain-Scott equation and the Brønsted relationship make the rather inaccurate assumption that all nucleophiles have the same reactivity with respect to a specific reaction site. There are several different categories of nucleophiles with different attacking atoms (e.g. oxygen, carbon, nitrogen) and each of these atoms has different nucleophilic characteristics.[3] The Edwards equation attempts to account for this additional parameter by introducing a polarizability term.

Edwards equations

The first generation of the Edwards equation[1] was

\log \frac{k}{k_0} = \alpha E_n + \beta H\,

where k and k0 are the rate constants for a nucleophile and a standard (H2O). H is a measure of the basicity of the nucleophile relative to protons, as defined by the equation:

\ H = pK_a + 1.74

where the pKa is that of the conjugate acid of the nucleophile and the constant 1.74 is the correction for the pKa of H3O+.

En is the term Edwards introduced to account for the polarizability of the nucleophile. It is related to the oxidation potential (E0) of the reaction 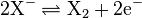\mathrm{2 X^- \rightleftharpoons X_2 + 2 e^-} (oxidative dimerization of the nucleophile) by the equation:

\ E_n = E_0 + 2.60

where 2.60 is the correction for the oxidative dimerization of water, obtained from a least-squares correlation of data in Edwards’ first paper on the subject.[1] α and β are then parameters unique to specific nucleophiles that relate the sensitivity of the substrate to the basicity and polarizability factors. [6] However, because some β’s appeared to be negative as defined by the first generation of the Edwards equation, which theoretically should not occur, Edwards adjusted his equation. The term En was determined to have some dependence on the basicity relative to protons (H) due to some factors that affect basicity also influencing the electrochemical properties of the nucleophile. To account for this, En was redefined in terms of basicity and polarizability (given as molar refractivity, RN):

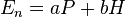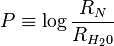
\ E_n = a P + b H where \ P \equiv \log \frac{R_N}{R_{H_20}}

The values of a and b, obtained by the method of least squares, are 3.60 and 0.0624 respectively.[2] With this new definition of En, the Edwards equation can be rearranged:

\log \frac{k}{k_0} = A P + B H\,

where A= αa and B = β + αb. However, because the second generation of the equation was also the final one, the equation is sometimes written as 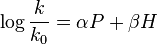\log \frac{k}{k_0} = \alpha P + \beta H\,, especially since it was republished in that form in a later paper of Edwards’,[7] leading to confusion over which parameters are being defined.

Significance

A later paper by Edwards and Pearson, following research done by Jencks and Carriuolo in 1960[8][9] led to the discovery of an additional factor in nucleophilic reactivity, which Edwards and Pearson called the alpha effect, [7] where nucleophiles with a lone pair of electrons on an atom adjacent to the nucleophilic center have enhanced reactivity. The alpha effect, basicity, and polarizability are still accepted as the main factors in determining nucleophilic reactivity. As such, the Edwards equation is applied in a qualitative sense much more frequently than in a quantitative one. [10] In studying nucleophilic reactions, Edwards and Pearson noticed that for certain classes of nucleophiles most of the contribution of nucleophilic character originated from their basicity, resulting in large β values. For other nucleophiles, most of the nucleophilic character came from their high polarizability, with little contribution from basicity, resulting in large α values. This observation led Pearson to develop his hard-soft acid-base theory, which is arguably the most important contribution that the Edwards equation has made to current understanding of organic and inorganic chemistry. [11] Nucleophiles, or bases, that were polarizable, with large α values, were categorized as “soft”, and nucleophiles that were non-polarizable, with large β and small α values, were categorized as “hard”.

The Edwards equation parameters have since been used to help categorize acids and bases as hard or soft, due to the approach’s simplicity.[12]

See also

References

  1. ↑ 1.0 1.1 1.2 Edwards, J.O. (1954). "Correlation of Relative Rates and Equilibria with a Double Basicity Scale". Journal of American Chemical Society 76 (6): 1540–1547. doi:10.1021/ja01635a021.
  2. ↑ 2.0 2.1 Edwards, J.O. (1956). "Polarizability, Basicity and Nucleophilic Character". Journal of American Chemical Society 78 (9): 1819–1820. doi:10.1021/ja01590a012.
  3. ↑ 3.0 3.1 Harris, J. Milton; McManus, Samuel P. (1987). Nucleophilicity 215. American Chemical Society. pp. 7–8. doi:10.1021/ba-1987-0215. ISBN 9780841209527.
  4. ↑ Swain, C. Gardner; Scott, Carleton B. (January 1953). "Quantitative Correlation of Relative Rates. Comparison of Hydroxide Ion with Other Nucleophilic Reagents toward Alkyl Halides, Esters, Epoxides and Acyl Halides". Journal of the American Chemical Society 75 (1): 141–147. doi:10.1021/ja01097a041.
  5. ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version:  (2006–) "Swain–Scott equation".
  6. ↑ Carroll, Felix (2010). Perspectives on Structure and Mechanism in Organic Chemistry (2 ed.). New Jersey: Wiley. pp. 506–507. ISBN 978-0470276105.
  7. ↑ 7.0 7.1 Edwards, J.O.; Pearson, Ralph G. (1962). "The Factors Determining Nucleophilic Reactivities". Journal of American Chemical Society 84 (1): 16–24. doi:10.1021/ja00860a005.
  8. ↑ Jencks, William P.; Carriuolo, Joan (April 1960). "Reactivity of Nucleophilic Reagents toward Esters". Journal of the American Chemical Society 82 (7): 1778–1786. doi:10.1021/ja01492a058.
  9. ↑ Jencks, William P.; Carriuolo, Joan (February 1960). "General Base Catalysis of the Aminolysis of Phenyl Acetate". Journal of the American Chemical Society 82 (3): 675–681. doi:10.1021/ja01488a044.
  10. ↑ Hudson, Michael J.; Laurence M. Harwood; Dominic M. Laventine; Frank W. Lewis (2013). "Use of Soft Heterocyclic N‑Donor Ligands To Separate Actinides and Lanthanides". Inorganic Chemistry 52 (7): 3414–3428. doi:10.1021/ic3008848.
  11. ↑ Pearson, Ralph G. (1963). "Hard and Soft Acids and Bases". J. Am. Chem. Soc. 85 (22): 3533–3539. doi:10.1021/ja00905a001.
  12. ↑ Yingst, Austin; MacDaniel, Darl H. (1967). "Use of the Edwards Equation to Determine Hardness of Acids". Inorganic Chemistry 6 (5): 1067–1068. doi:10.1021/ic50051a051.
This article is issued from Wikipedia - version of the Monday, May 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.