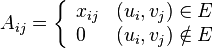Edmonds matrix

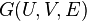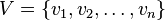In graph theory, the Edmonds matrix $A$ of a balanced bipartite graph $G(U, V, E)$ with sets of vertices $U = \{u_1, u_2, \dots , u_n \}$ and $V = \{v_1, v_2, \dots , v_n\}$ is defined by

A_{ij} = \left\{ \begin{array}{ll} x_{ij} & (u_i, v_j) \in E \\ 0 & (u_i, v_j) \notin E \end{array}\right.

where the x_ij are indeterminates. One application of the Edmonds matrix of a bipartite graph is that the graph admits a perfect matching if and only if the polynomial det(A_ij) in the x_ij is not identically zero. Furthermore, the number of perfect matchings is equal to the number of monomials in the polynomial det(A), and is also equal to the permanent of $A$ . In addition, rank of $A$ is equal to the maximum matching size of $G$ .

The Edmonds matrix is named after Jack Edmonds. The Tutte matrix is a generalisation to non-bipartite graphs.

References

R. Motwani, P. Raghavan (1995). Randomized Algorithms. Cambridge University Press. p. 167.
Allen B. Tucker (2004). Computer Science Handbook. CRC Press. p. 12.19. ISBN 1-58488-360-X.

This article is issued from Wikipedia - version of the Monday, October 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.