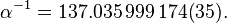Eddington number

Arthur Stanley Eddington (1882–1944)

In astrophysics, the Eddington number, N_Edd, is the number of protons in the observable universe. The term honors the British astrophysicist Arthur Eddington, who in 1938 was the first to propose a value of N_Edd and to explain why this number might be important for cosmology and the foundations of physics.

History

Eddington argued that the value of the fine-structure constant, α, could be obtained by pure deduction. He related α to the Eddington number, which was his estimate of the number of protons in the universe.^[1] This led him in 1929 to conjecture that α was exactly 1/137. Other physicists did not adopt this conjecture and did not accept his argument.

In the late 1930s, the best experimental value of the fine-structure constant, α, was approximately 1/136. Eddington then argued, from aesthetic and numerological considerations, that α should be exactly 1/136. He devised a "proof" that N_Edd = 136×2²⁵⁶, or about 1.57×10⁷⁹. Some estimates of N_Edd point to a value of about 10⁸⁰. These estimates assume that all matter can be taken to be hydrogen and require assumed values for the number and size of galaxies and stars in the universe.^[2]

Attempts to find a mathematical basis for this dimensionless constant have continued up to the present time.

In the 1938 Tarner Lecture at Trinity College, Cambridge, Eddington averred that:

I believe there are 15 747 724 136 275 002 577 605 653 961 181 555 468 044 717 914 527 116 709 366 231 425 076 185 631 031 296 protons in the universe and the same number of electrons.^[3]

This large number was soon named the "Eddington number."

Shortly thereafter, improved measurements of α yielded values closer to 1/137, whereupon Eddington changed his "proof" to show that α had to be exactly 1/137.^[4]

Recent theory

The most precise value of α (obtained experimentally in 2012) is:^[5]

Consequently, no one maintains any longer that α is the reciprocal of an integer. Nor does anyone take seriously a mathematical relationship between α and N_Edd.

On possible roles for N_Edd in contemporary cosmology, especially its connection with large number coincidences, see Barrow (2002) (easier) and Barrow and Tipler (1986: 224–31) (harder).

See also

• Eddington–Dirac number
• Eddington number (cycling)
• One-electron universe
• Universe

References

Bibliography

• John D. Barrow (2002). The Constants of Nature from Alpha to Omega: The Numbers That Encode the Deepest Secrets of the Universe. Pantheon Books. ISBN 0-375-42221-8. 
• John D. Barrow & Frank J. Tipler (1986). The Anthropic Cosmological Principle. London: Oxford University Press. 
• Dingle, H. (1954). The Sources of Eddington's Philosophy. London: Cambridge University Press. 
• Arthur Eddington (1928). The Nature of the Physical World. London: Cambridge University Press. 
• -------- (1935). New Pathways in Science. London: Cambridge University Press. 
• -------- (1939). The Philosophy of Physical Science. London: Cambridge University Press. 
• -------- (1946). Fundamental Theory. London: Cambridge University Press. 
• Kilmister, C.W. & Tupper, B.O.J. (1962). Eddington's Statistical Theory. London: Oxford University Press. 
• Mohr, P.J. & Taylor, B.N. (2005). "CODATA recommended values of the fundamental phh". Reviews of Modern Physics 77: 1–107. Bibcode:2005RvMP...77....1M. doi:10.1103/RevModPhys.77.1. 
• Slater, N.B. (1957). Development and Meaning in Eddington's Fundamental Theory. London: Cambridge University Press. 
• Whittaker, E.T. (1951). Eddington's Principle in the Philosophy of Science. London: Cambridge University Press. 
• -------- (1958). From Euclid to Eddington. New York: Dover.