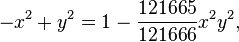EdDSA
In public-key cryptography, Edwards-curve Digital Signature Algorithm (EdDSA) is a digital signature scheme using a variant of Schnorr signature based on Twisted Edwards curves. It is designed to be faster than existing digital signature schemes without sacrificing security. It was developed by a team including Daniel J. Bernstein, Niels Duif, Tanja Lange, Peter Schwabe, and Bo-Yin Yang.[1]
Ed25519
Ed25519 is a specific implementation of EdDSA using the Twisted Edwards curve:
over the prime field defined by the prime number 2255 − 19. This curve is birationally equivalent to the Montgomery curve known as Curve25519. The equivalence is 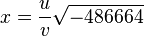 and
and 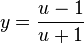 .[1][2]
.[1][2]
Features
Performance
The Bernstein team has optimized Ed25519 for the x86-64 Nehalem/Westmere processor family. Verification can be performed in batches of 64 signatures for even greater throughput. Ed25519 is intended to provide attack resistance comparable to quality 128-bit symmetric ciphers. Public keys are 256 bits in length and signatures are twice that size.
Secure coding
Security features of Ed25519 include elimination of branch operations and array indexing steps that depend on secret data, so as to defeat many side channel attacks.
Like other digital signature algorithms, EdDSA requires a secret value, or nonce, unique to each signature. However EdDSA calculates this nonce deterministically, as the hash of the secret key and the message, rather than using a randomly generated number. This reduces the risk of a random number generator attack, but does not completely eliminate it, since high quality random numbers are still needed for key generation.
Software
Notable uses of Ed25519 include OpenSSH, GnuPG and various alternatives, and the signify tool by OpenBSD.[3]
- SUPERCOP reference implementation (C language with inline assembler)
- Slow but concise alternate implementation, does not include side-channel attack protection[4] (Python)
- NaCl
- CryptoNote cryptocurrency protocol
- wolfSSL[5]
See also
References
- 1 2 Bernstein, Daniel J.; Duif, Niels; Lange, Tanja; Schwabe, Peter; Bo-Yin Yang (2012). "High-speed high-security signatures" (PDF). Journal of Cryptographic Engineering 2 (2): 77–89. doi:10.1007/s13389-012-0027-1.
- ↑ Bernstein, Daniel J.; Lange, Tanja (2007). Kurosawa, Kaoru, ed. Faster addition and doubling on elliptic curves. Advances in cryptology—ASIACRYPT. Lecture Notes in Computer Science. Berlin: Springer. pp. 29–50. doi:10.1007/978-3-540-76900-2_3. ISBN 978-3-540-76899-9. MR 2565722.
- ↑ "Things that use Ed25519". Retrieved 6 January 2015.
- ↑ "Alternate implementations". Retrieved 17 November 2014.
- ↑ https://www.wolfssl.com/wolfSSL/Products-wolfssl.html