Ecosystem model
An ecosystem model is an abstract, usually mathematical, representation of an ecological system (ranging in scale from an individual population, to an ecological community, or even an entire biome), which is studied to gain understanding of the real system.[2]
Using data gathered from the field, ecological relationships — such as the relation of sunlight and water availability to photosynthetic rate, or that between predator and prey populations — are derived, and these are combined to form ecosystem models. These model systems are then studied in order to make predictions about the dynamics of the real system. Often, the study of inaccuracies in the model (when compared to empirical observations) will lead to the generation of hypotheses about possible ecological relations that are not yet known or well understood. Models enable researchers to simulate large-scale experiments that would be too costly or unethical to perform on a real ecosystem. They also enable the simulation of ecological processes over very long periods of time (i.e. simulating a process that takes centuries in reality, can be done in a matter of minutes in a computer model).[3]
Ecosystem models have applications in a wide variety of disciplines, such as natural resource management,[4] ecotoxicology and environmental health,[5][6] agriculture,[7] and wildlife conservation.[8] It has also been applied to archaeology with varying degrees of success, through attempts to combine ecological models and archaeological models to explain mobility, diversity, etc. of stone tools [9]
Types of models
There are two major types of ecological models, which are generally applied to different types of problems: (1) analytic models and (2) simulation/computational models. Analytic models are often more complex mathematically, and work best when dealing with relatively simple (often linear) systems, specifically those that can be accurately described by a set of mathematical equations whose behavior is well known. Simulation models on the other hand, use numerical techniques to solve problems for which analytic solutions are impractical or impossible. Simulation models tend to be more widely used, and are generally considered more ecologically realistic, while analytic models are valued for their mathematical elegance and explanatory power.[10][11][12] Ecopath is a powerful software system which uses simulation and computational methods to model marine ecosystems. It is widely used by marine and fisheries scientists as a tool for modelling and visualising the complex relationships that exist in real world marine ecosystems.[13][14][15]
Model design

The process of model design begins with a specification of the problem to be solved, and the objectives for the model.[17]
Ecological systems are composed of an enormous number of biotic and abiotic factors that interact with each other in ways that are often unpredictable, or so complex as to be impossible to incorporate into a computable model. Because of this complexity, ecosystem models typically simplify the systems they are studying to a limited number of components that are well understood, and deemed relevant to the problem that the model is intended to solve.[18][19]
The process of simplification typically reduces an ecosystem to a small number of state variables and mathematical functions that describe the nature of the relationships between them.[20] The number of ecosystem components that are incorporated into the model is limited by aggregating similar processes and entities into functional groups that are treated as a unit.[21][22]
After establishing the components to be modeled and the relationships between them, another important factor in ecosystem model structure is the representation of space used. Historically, models have often ignored the confounding issue of space. However, for many ecological problems spatial dynamics are an important part of the problem, with different spatial environments leading to very different outcomes. Spatially explicit models (also called "spatially distributed" or "landscape" models) attempt to incorporate a heterogeneous spatial environment into the model.[23][24][25] A spatial model is one that has one or more state variables that are a function of space, or can be related to other spatial variables.[26]
Validation
After construction, models are validated to ensure that the results are acceptably accurate or realistic. One method of validation is to test the model with multiple sets of data that are independent of the actual system being studied. This is important since certain inputs can cause a faulty model to output correct results. Another method of validation is to compare the model's output with data collected from field observations. Researchers frequently specify beforehand how much of a disparity they are willing to accept between parameters output by a model and those computed from field data.[27][28][29][30][31]
Example: The Lotka–Volterra equations
One of the earliest,[32] and most well-known, ecological models is the predator-prey model of Alfred J. Lotka (1925)[33] and Vito Volterra (1926).[34] This model takes the form of a pair of ordinary differential equations, one representing a prey species, the other its predator.
where,
|
|
Volterra originally devised the model to explain fluctuations in fish and shark populations observed in the Adriatic Sea after the First World War (when fishing was curtailed). However, the equations have subsequently been applied more generally.[35] Although simple, they illustrate some of the salient features of ecological models: modelled biological populations experience growth, interact with other populations (as either predators, prey or competitors) and suffer mortality.
A credible, simple alternative to the Lotka-Volterra predator-prey model and its common prey dependent generalizations is the ratio dependent or Arditi-Ginzburg model.[36] The two are the extremes of the spectrum of predator interference models. According to the authors of the alternative view, the data show that true interactions in nature are so far from the Lotka-Volterra extreme on the interference spectrum that the model can simply be discounted as wrong. They are much closer to the ratio dependent extreme, so if a simple model is needed one can use the Arditi-Ginzburg model as the first approximation.[37]
See also
References
- ↑ Fasham, M. J. R.; Ducklow, H. W.; McKelvie, S. M. (1990). "A nitrogen-based model of plankton dynamics in the oceanic mixed layer". Journal of Marine Research 48: 591–639. doi:10.1357/002224090784984678.
- ↑ Hall, Charles A.S. & Day, John W. (1990). Ecosytem Modeling in Theory and Practice: An Introduction with Case Histories. University Press of Colorado. pp. 7–8. ISBN 0-87081-216-5.
- ↑ Hall & Day, 1990: pp. 13-14
- ↑ Dale, Virginia (2003). "Opportunities for Using Ecological Models for Resource Management". Ecological modeling for resource management. Springer. p. 3. ISBN 978-0-387-95493-6.
- ↑ Pastorok, Robert A. (2002). "Introduction". Ecological modeling in risk assessment: chemical effects on populations, ecosystems, and landscapes. CRC Press. p. 7. ISBN 978-1-56670-574-5.
- ↑ Forbes, Valery E. (2009). "The Role of Ecological Modeling in Risk Assessments Seen From an Academic's Point of View". In Thorbek, Pernille. Ecological Models for Regulatory Risk Assessments of Pesticides: Developing a Strategy for the Future. CRC Press. p. 89. ISBN 978-1-4398-0511-4.
- ↑ Palladino, Paolo (1996). "Ecological Modeling and Integrated Pest Management". Entomology, ecology and agriculture: the making of scientific careers in North America, 1885-1985. Psychology Press. p. 153. ISBN 978-3-7186-5907-4.
- ↑ Millspaugh, Joshua J. et al. (2008). "General Principles for Developing Landscape Models for Wildlife Conservation". Models for planning wildlife conservation in large landscapes. Academic Press. p. 1. ISBN 978-0-12-373631-4.
- ↑ Marwick, Ben. Multiple Optima in Hoabinhian flaked stone artefact palaeoeconomics and palaeoecology at two archaeological sites in Northwest Thailand. Journal of Anthropological Archaeology 32.4 (2013): 553-564.
- ↑ Jørgensen, Sven Erik (1996). Handbook of environmental and ecological modeling. CRC Press. pp. 403–404. ISBN 978-1-56670-202-7.
- ↑ Grant, William Edward & Swannack, Todd M. (2008). Ecological modeling: a common-sense approach to theory and practice. John Wiley & Sons. p. 74. ISBN 978-1-4051-6168-8.
- ↑ Hall, Charles A.S. & Day, John W. (1990). Ecosytem Modeling in Theory and Practice: An Introduction with Case Histories. University Press of Colorado. p. 9. ISBN 0-87081-216-5.
- ↑ Pauly D, Christensen V, and Walters C (2000) Ecopath, Ecosim, and Ecospace as tools for evaluating ecosystem impact of fisheries ICES Journal of Marine Science, 57: 697–706. doi:10.1006/jmsc.2000.0726
- ↑ Christensen V and Walters C (2004) Ecopath with Ecosim: methods, capabilities and limitations Ecological modelling, 172: 109–139.
- ↑ Christensen V (2009) "The future of Ecopath" In: Palomares, MLD, Morissette L, Cisneros-Montemayor A, Varkey D, Coll M, Piroddi C (Eds), Ecopath 25 Years Conference Proceedings: Extended Abstracts, Fisheries Centre Research Reports 17(3): 159–160. University of British Columbia.
- ↑ Odum, H.T. (1971). Environment, Power, and Society. Wiley-Interscience New York, N.Y.
- ↑ Soetaert, Karline & Herman, Peter M.J. (2009). A practical guide to ecological modelling: using R as a simulation platform. Springer. p. 11. ISBN 978-1-4020-8623-6.
- ↑ Gillman, Michael & Hails, Rosemary (1997). An introduction to ecological modelling: putting practice into theory. Wiley-Blackwell. p. 4. ISBN 978-0-632-03634-9.
- ↑ Müller, Felix et al. (2011). "What are the General Conditions Under Which Ecological Models Can Be Applied". In Jopp, Fred et al. Modeling Complex Ecological Dynamics. Springer. pp. 13–14. ISBN 978-3-642-05028-2.
- ↑ Hall & Day, 1990: p. 21
- ↑ Hall & Day, 1990: p. 19
- ↑ Buschke, F.T. & Seaman, M.T. 2011. Functional feeding groups as a taxonomic surrogate for a grassland arthropod assemblage. African Invertebrates 52 (1): 217-228.
- ↑ McCallum, Hamish (2000). "Spatial Parameters". Population parameters: estimation for ecological models. Wiley-Blackwell. p. 184. ISBN 978-0-86542-740-2.
- ↑ Tenhunen, John D. et al, eds. (2001). Ecosystem approaches to landscape management in Central Europe. Springer. pp. 586–587. ISBN 978-3-540-67267-8.
- ↑ Ball, George L. (1999). "Ecological modeling". Encyclopedia of environmental science. Springer. p. 154. ISBN 978-0-412-74050-3.
- ↑ Sklar, Fred H. & Hunsaker, Carolyn T. (2001). "The Use and Uncertainties of Spatial Data for Landscape Models: An Overview with Examples from the Florida Everglades". In Hunsaker, Carolyn T. Spatial uncertainty in ecology: implications for remote sensing and GIS applications. Springer. p. 15. ISBN 978-0-387-95129-4.
- ↑ Jørgensen, Sven Erik & Bendoricchio, G. (2001). Fundamentals of ecological modelling. Gulf Professional Publishing. p. 79. ISBN 978-0-08-044028-6.
- ↑ Pastorok, Robert A. (2002). "Introduction". Ecological modeling in risk assessment: chemical effects on populations, ecosystems, and landscapes. CRC Press. p. 22. ISBN 978-1-56670-574-5.
- ↑ Shifley, S.R. (2008). "Validation of Landscape-Scale Decision Support Models That Predict Vegetation and Wildlife Dynamics". In Millspaugh, Joshua J. & Thompson, Frank Richard. Models for planning wildlife conservation in large landscapes. Academic Press. p. 419. ISBN 978-0-12-373631-4.
- ↑ Voinov, Alexey (2008). Systems Science and Modeling for Ecological Economics. Academic Press. p. 131. ISBN 978-0-12-372583-7.
- ↑ Reuter, Hauke et al. (2011). "How Valid Are Model Results? Assumptions, Validity Range and Documentation". In Jopp, Fred et al. Modeling Complex Ecological Dynamics. Springer. p. 325. ISBN 978-3-642-05028-2.
- ↑ Earlier work on smallpox by Daniel Bernoulli and human overpopulation by Thomas Malthus predates that of Lotka and Volterra, but is not strictly ecological in nature
- ↑ Lotka, A. J. (1925). The Elements of Physical Biology. Williams & Williams Co., Baltimore, USA.
- ↑ Volterra, V. (1926). "Fluctuations in the abundance of a species considered mathematically". Nature 118 (2983): 558–560. Bibcode:1926Natur.118..558V. doi:10.1038/118558a0.
- ↑ Begon, M.; Harper, J. L.; Townsend, C. R. (1988). Ecology: Individuals, Populations and Communities. Blackwell Scientific Publications Inc., Oxford, UK.
- ↑ Arditi, R. and Ginzburg, L.R. (1989) "Coupling in predator-prey dynamics: ratio dependence" Journal of Theoretical Biology, 139: 311–326.
- ↑ Arditi, R. and Ginzburg, L.R. (2012) How Species Interact: Altering the Standard View on Trophic Ecology Oxford University Press. ISBN 9780199913831.
External links
- Ecological modelling resources (ecobas.org)
- Exposure Assessment Models United States Environmental Protection Agency
- Ecotoxicology & Models (ecotoxmodels.org)
| ||||||||||||||||||||||||||||||||||

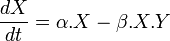
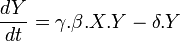
 is the number/concentration of the prey species;
is the number/concentration of the prey species;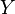 is the number/concentration of the predator species;
is the number/concentration of the predator species; is the prey species' growth rate;
is the prey species' growth rate;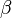 is the predation rate of
is the predation rate of  is the
is the 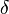 is the mortality rate of the predator species
is the mortality rate of the predator species